下面我們來介紹電磁感應定律。電磁感應定律實際上有兩部分組成，第一部分是法拉第電磁感應定律，第二個是楞次定律。研究電磁感應定律的基本方法，用實驗的方法來抓住磁通變化這個核心問題進行討論。下面我們來觀察條形磁鐵接近和離開線圈的同時，電流指針變化情況。

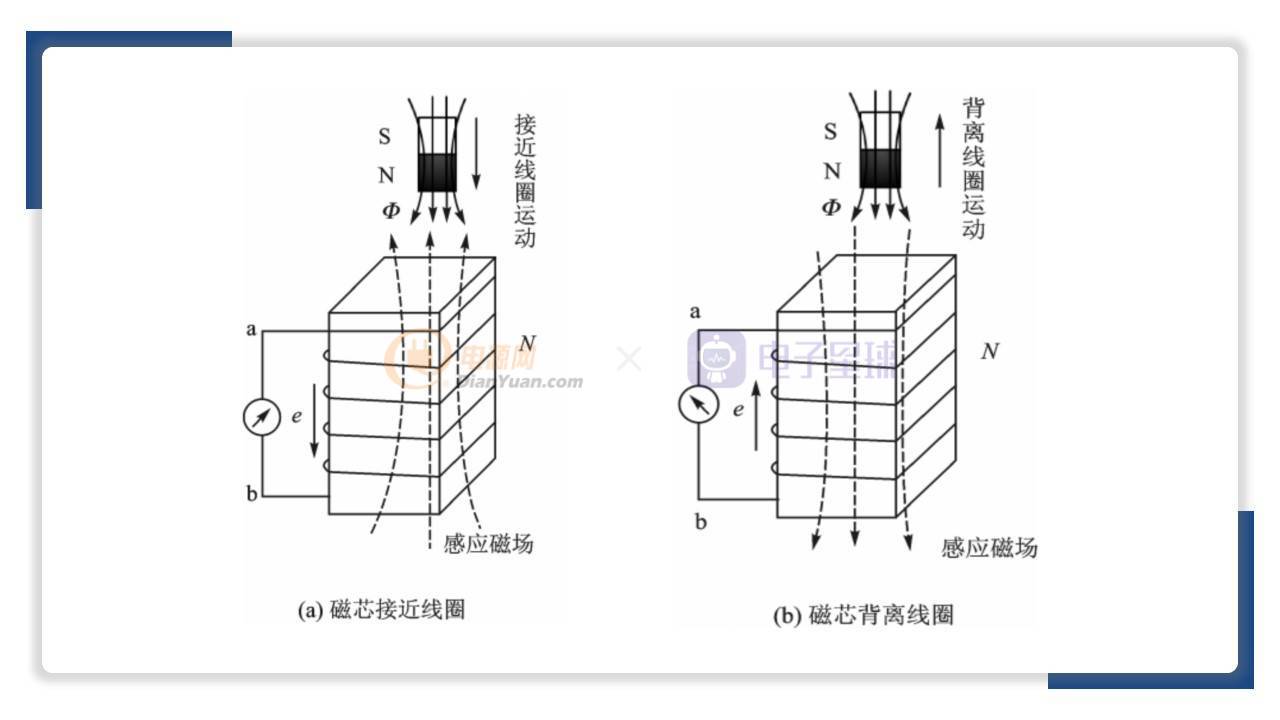
下面我們研究電磁感應定律。如果將一個條形磁鐵穿向線圈中，那么既然線圈兩端的電流表指針即將發生偏轉，如果磁鐵不動，而電流表指針也不動，如果將磁鐵又從線圈中取出，電流表指針與插入時偏轉方向正好相反。由此可見，當通過線圈的磁通發生變化時，不論是什么原因引起磁通的變化，都會在線圈的兩端產生感應電動勢，而且磁通變化越快，感應電動勢就越大，指針偏轉的角度就越大。因此感應電動勢大小，正比磁通的變化率。

根據前面的實驗，那么我們定義如果是對于一匝線圈，也就單匝線圈，感應電動勢的大小就是磁通的變化率，如果有n匝線圈也就多匝線圈的時候，感應電動勢的大小

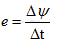
，其中ΔΨ=ΔNΦ，我們把Ψ=NΦ稱為磁鏈。

所以n匝線圈的感應電動勢是單匝線圈的感應電動勢的n倍，所以公式表明了單匝線圈匝鏈的磁通在1秒內變化1Wb時，線圈的端點電壓為1V。法拉第電磁感應定律，解決了感應電動勢與磁通變化率之間的關系，但是并沒有說明感應電動勢的方向。

法拉第電磁感應定律，解決了磁通的變化率與感應電動勢之間的關系。但沒有解決反應電動勢的方向。那么解決感應電動勢的方向是什么呢？就是楞次定律。

感應電動勢方向的是楞次定律，是這樣子描述的：感生電流總是試圖維持原磁通不變，這就是楞次定律。那么楞次定律這樣的一個定義，還有沒有其他解釋？我們可以總結出來和牛頓的慣性定律一樣，他是磁場的慣性定律，另外一個維持原磁通不變，就是阻礙變化。

下面我們來研究電磁能量的關系。

那么為什么要討論能量呢？我們從源頭開始分析，有電流就會產生磁場，載流導體在磁場當中又會受到力的作用。我們知道有力就會產生運動，有運動就要做功，要做功就必須要有能量，有能量就要有存儲的地方，移動能量需要時間和場地就會引起狀態的改變。我想這就是為什么要討論能量的原因。

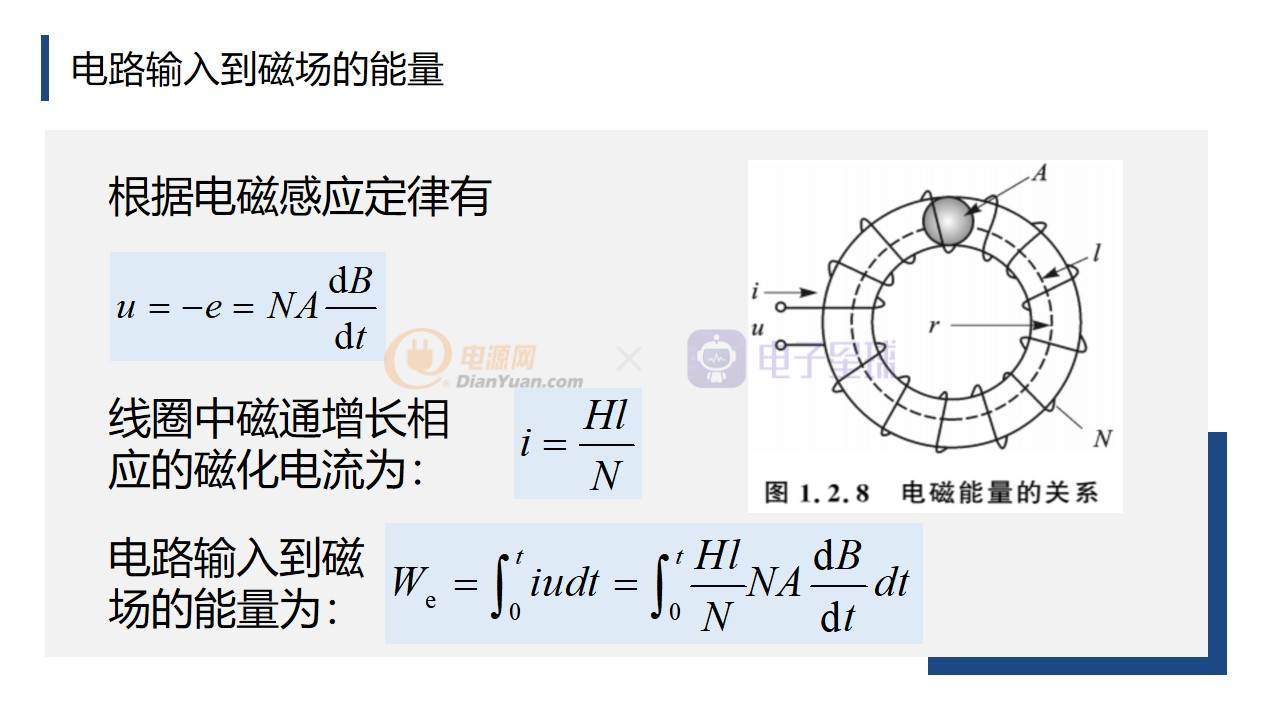
下面我們來研究電路輸入到磁場的能量。

請看右圖，環形線圈它的截面積是A，它的磁性的平均周長是l，半徑是r，在環形磁芯上繞了N匝線圈，線圈的兩端接到電源，電源的電壓為u，這樣子就有電流流入線圈。根據電磁感應定律，輸入電壓

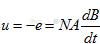
也就是說線圈中磁感應密度的變化量。那么線圈中磁通的增長相應的磁化電流為

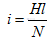
那么電路輸入到磁場的能量為

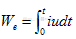
把i和u的表達式代入式中就是

。

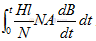
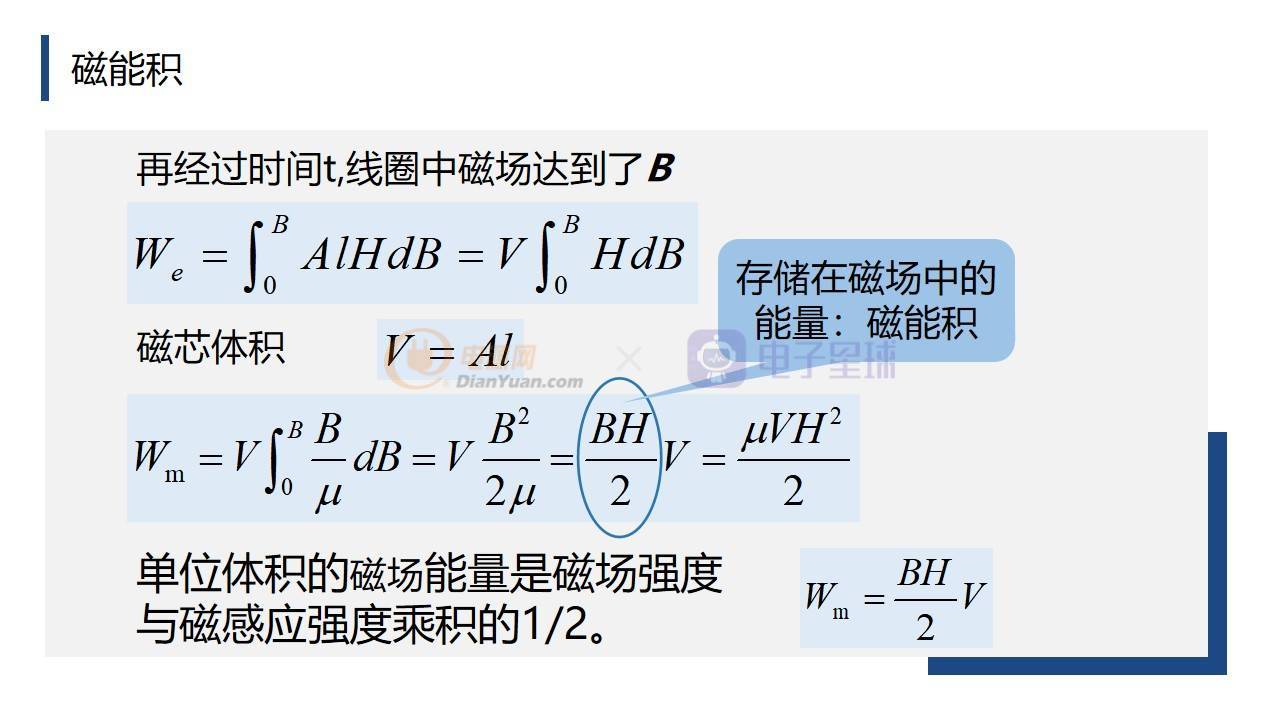
前面我們介紹了由電路輸入到磁場的能量為We，如果在經過時間t以后，線圈中的磁場達d，那么我們對We的求解可以更換積分變量，由變量t改為B，所以得到了

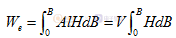
那么其中唯一的話是磁性的體積，它的大小等于Al，那么通過計算以后我們又得到了從電路來的能量直接存儲到磁性當中，也就是說存儲的磁場能量，磁場力量用Wm表示，

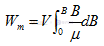
那么經過分析計算以后等于

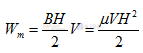
那么我們把BH/2存儲在磁場中能量我們稱為磁能積。那么單位體積的磁場能量是磁場強度與磁感應強度乘積的1/2，

。

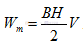
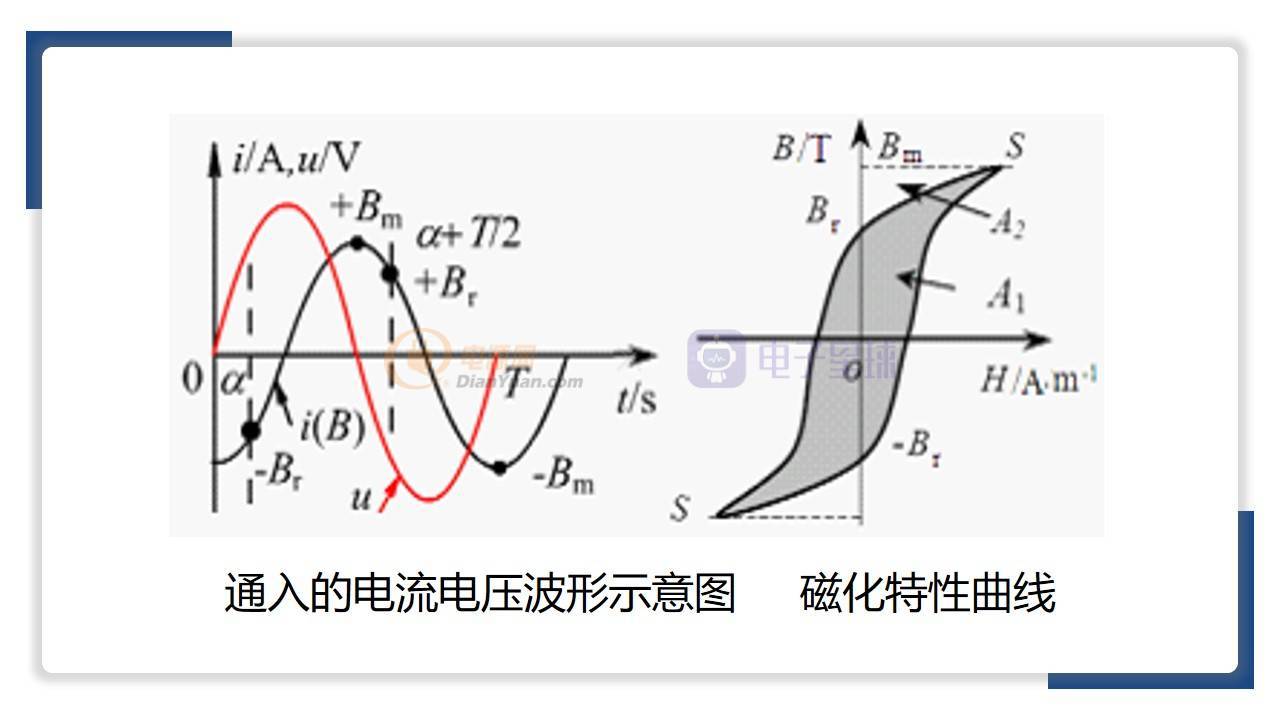
前面我們介紹了儲存在磁場當中能量的計算方法。我們看一下，如果環形磁芯它的輸入端接到了正斜波電壓處相位是0的這樣的一個電壓波形，那么在磁線當中磁化的時候產生的磁感應強度會適合一個角度α。那么假設我們是積分周期從-Br積分到+Bm，再從+Bm來積分到+Br，那么對應的磁化特新曲線就是我們右圖說-Br積分到S，那么這個曲線包圍的面積就是A1的面積，如果從S點由去磁去到+Br那個時候和縱軸包圍的面積就是A2這個面積，這么能量時回送給電源的能量，而A1這個面積是從電路從電源獲得的能量。

下面我們對本章的學習做一些小結，主要有這兩個方面。

第一，只要有電流，不管是恒定的還是變化的，都會產生磁場。

第二，磁場用磁力線形象的描述，磁力線是無頭無尾的光滑曲線，其切線方向表示磁場方向，在磁鐵的內部，磁力線是由南極指向北極，在外部是由北極指向南極。