本文轉(zhuǎn)自徐飛翔的“【多視角立體視覺系列】 幾何變換的層次——投影變換，仿射變換，度量變換和歐幾里德變換”

版權(quán)聲明：本文為博主原創(chuàng)文章，遵循CC 4.0 BY-SA版權(quán)協(xié)議，轉(zhuǎn)載請(qǐng)附上原文出處鏈接和本聲明

你不可不知的幾何元素研究一個(gè)幾何問題，一般可以通過兩種方式進(jìn)行，第一種是進(jìn)行“純粹”的幾何研究，也就是說(shuō)這種研究應(yīng)該是和所謂坐標(biāo)系一點(diǎn)關(guān)系都沒有的，在不使用任何代數(shù)方法的情況下，用幾何公理推出其他定理，也就是傳統(tǒng)的歐幾里德幾何；第二種，我們其實(shí)也是很熟悉的，就是解析幾何，由笛卡爾提出并流行，在這種方法中，我們用代數(shù)元素，比如向量去表示幾何的點(diǎn)，線，面，用點(diǎn)乘，叉乘去表示元素的一系列操作，從而可以用代數(shù)方法進(jìn)行幾何關(guān)系的推理。由于現(xiàn)在計(jì)算機(jī)本質(zhì)上是對(duì)數(shù)值進(jìn)行計(jì)算，因此通過解析幾何的方法，也就是代數(shù)法更容易設(shè)計(jì)計(jì)算機(jī)可以解決的算法，因此本文首先要對(duì)幾何元素進(jìn)行代數(shù)表示。

正如我們?cè)谇把运f(shuō)的，幾何元素?zé)o非就是點(diǎn)線面，我們?cè)赱3]中其實(shí)已經(jīng)初步探討過為什么要引進(jìn)齊次坐標(biāo)這個(gè)概念，然而，這里希望重新進(jìn)行解釋，因此我們將從線的代數(shù)表示開始說(shuō)起。

直線我們由中學(xué)的知識(shí)，知道線在二維空間可以表示為：

這個(gè)線完全由的組合給決定了，因此可以用這個(gè)向量表示這個(gè)直線，我們又注意到對(duì)于該線來(lái)說(shuō)，式子(1.2)同樣成立：

而顯然，表示的是同一個(gè)直線，于是我們知道，對(duì)于這條直線，其表示有無(wú)窮多種，此尺度大小也就是k 只要不為0都是等價(jià)的。 特別的，如果那么我們的原先的c就變?yōu)榱?，于是該直線變成了，其實(shí)只需要兩個(gè)變量就可以決定一個(gè)2D直線了。

需要注意的是，本文用到的每個(gè)幾何元素都是以列向量的形式表示的，也就是說(shuō)是一個(gè)列向量，而其轉(zhuǎn)置才是行向量。

點(diǎn)怎么表示一個(gè)在線上的點(diǎn)呢？既然點(diǎn)在線上，那么自然地，滿足式子(1.1)，如果把這個(gè)式子寫成向量乘法的形式，我們有：

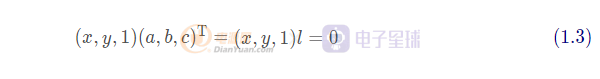
說(shuō)明點(diǎn)在該線上。為什么一個(gè)二維的點(diǎn)，會(huì)需要在尾巴上多一個(gè)1去表示呢？顯然，這個(gè)是我們之前提到的齊次坐標(biāo)系[3]，但是為什么要這個(gè)坐標(biāo)系，我們雖然之前也提到過，但是本文后面還會(huì)繼續(xù)解釋的。

面

面，一般是存在于三維幾何中的概念，其可以表達(dá)為：

也就是說(shuō)，面可以用表示，而在面上的點(diǎn)，同樣的是在齊次坐標(biāo)下表示的，為 。

我們發(fā)現(xiàn)到，無(wú)論是點(diǎn)線面，都可以通過一個(gè)向量進(jìn)行表示。

線的相交考慮在二維情況下，我們要如何表示兩個(gè)線的交點(diǎn)呢？假如給定兩個(gè)直線 , ，定義出向量? ，其中的表示的是叉乘。由向量叉乘的幾何意義我們知道，其得到的是正交于兩個(gè)向量的向量，顯然，這兩個(gè)向量中的任意一個(gè)向量正交于l，也就是有也就是，也就是說(shuō)向量x xx同時(shí)通過了這兩條線，顯然，他就是交點(diǎn)。

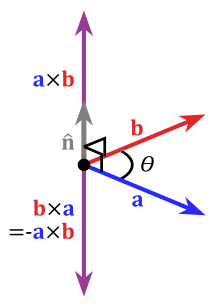
于是我們知道，兩個(gè)線的交點(diǎn)就是兩個(gè)線表示的向量的叉乘：

其中的，而是一個(gè)矩陣，為：

圓錐線和二次曲錐面圓錐線和二次曲錐面在計(jì)算機(jī)視覺的幾何變換中特別常見，鑒于其篇幅較長(zhǎng)，我獨(dú)立成一篇博文，見[4]。當(dāng)然，你也可以先不管這個(gè)幾何元素，直到我們后面提到了IAC, Image of Absolute Conic的時(shí)候在回過頭復(fù)習(xí)它。

說(shuō)在前面——理想點(diǎn)和無(wú)限遠(yuǎn)處的線和面我們?cè)赱3]中曾經(jīng)討論過理想點(diǎn)（Ideal point）這個(gè)概念，簡(jiǎn)單來(lái)說(shuō)就是平行線交于無(wú)窮遠(yuǎn)處，這個(gè)定義可能不夠直觀，我們借助解析幾何，用代數(shù)的形式，在齊次坐標(biāo)的幫助下去定義它。考慮到兩個(gè)平行線，那么可以表示為，那么由我們上面討論的，我們知道兩個(gè)平行線的交點(diǎn)，即便它們是平行線，也可以用叉乘去描述，如 ，忽略這個(gè)尺度因子，我們發(fā)現(xiàn)其交點(diǎn)是 。如果把這個(gè)齊次坐標(biāo)轉(zhuǎn)變?yōu)榉驱R次坐標(biāo)，我們有 ，這個(gè)顯然是無(wú)法計(jì)算的，這也意味著平行線的交點(diǎn)都在無(wú)窮遠(yuǎn)處的點(diǎn)上，為了在歐幾里德空間中表示這種無(wú)窮遠(yuǎn)處的點(diǎn)，非齊次坐標(biāo)系是無(wú)能為力的，我們只能引入齊次坐標(biāo)系，也就是在歐幾里德空間坐標(biāo)的基礎(chǔ)上，在最后一維再加上一個(gè)維度。

（PS： 為什么非得在歐幾里德空間里面，以統(tǒng)一的方式去表達(dá)平行線和非平行線的方程呢？那是因?yàn)椋队白儞Q中，特別是透視變換中，存在將“平行線”變換成“非平行線”，或者將“非平行線”變換成“平行線”的操作，如果不能進(jìn)行統(tǒng)一表示，那么就不能用統(tǒng)一的形式去數(shù)學(xué)形式化這個(gè)過程了。）

Fig 2.1 即便是平行線也會(huì)在無(wú)限遠(yuǎn)處相交，這個(gè)相交點(diǎn)稱之為理想點(diǎn)。

為了考慮平行線的相交的情況，對(duì)于二維平面，我們?cè)跓o(wú)限遠(yuǎn)處假設(shè)出了無(wú)限遠(yuǎn)的線(line at infinity)，表示為。對(duì)于三維空間來(lái)說(shuō)，我們?cè)跓o(wú)限遠(yuǎn)處假設(shè)出了無(wú)限遠(yuǎn)的平面(plane at infinity)，表示為。我們嘗試用代數(shù)的方式表示這兩個(gè)元素，我們知道無(wú)限遠(yuǎn)處的點(diǎn)可以表示為（三維情況下要多加一個(gè)維度），而無(wú)限遠(yuǎn)處的點(diǎn)應(yīng)該在無(wú)限遠(yuǎn)處的平面或者線上，那么有：

這樣就不難得到，這兩個(gè)元素的一種表達(dá)方式為：

事實(shí)上，根據(jù)齊次坐標(biāo)的性質(zhì)，我們?nèi)菀字肋@兩個(gè)元素的任意表達(dá)方式都是等價(jià)的。

走得更進(jìn)一步——討論幾何變換

在之前的章節(jié)中，我們用代數(shù)的方式定義了很多幾何元素，這些幾何元素都是在幾何變換中的基本變換單元，在本章節(jié)，我們將正式起航，討論在空間中幾何變換。我們首先要考慮的是最為熟悉的歐幾里德空間，我們?nèi)粘Ｉ钜话憧梢越闅W幾里德空間，可以定義出一個(gè)原點(diǎn)，然后兩個(gè)或者三個(gè)互為正交的坐標(biāo)軸，然后客體，也就是我們要研究的物體主體就在這個(gè)歐式空間中移動(dòng)，旋轉(zhuǎn)等，我們會(huì)發(fā)現(xiàn)，這里如果把客體看成是一個(gè)剛體，也就是自身不發(fā)生形變的物體，那么客體在歐式空間的旋轉(zhuǎn)，平移等，都是所謂的歐幾里德變換(Euclidean transformations)。當(dāng)然這章暫時(shí)只是概念上的辨析，就先不拿出變換公式搞暈各位讀者吧。

好的我們繼續(xù)，注意到，雖然歐幾里德空間坐標(biāo)系一般都有一個(gè)原點(diǎn)，有相應(yīng)的坐標(biāo)軸，但是這個(gè)原點(diǎn)并沒有什么特別的地方，坐標(biāo)軸的方向也沒有任何特別的地方，都是我們研究人員為了方便自己設(shè)定的，事實(shí)上，這個(gè)原點(diǎn)和坐標(biāo)軸我們可以任意的指定，任何一個(gè)在有限空間內(nèi)的，可以用代數(shù)表達(dá)的原點(diǎn)和坐標(biāo)軸方向我們都可以指定，只要滿足約束條件：

在有限的空間內(nèi)的，也就是每個(gè)原點(diǎn)的分量值都是實(shí)數(shù)；

坐標(biāo)軸互相正交

歐幾里德空間里面的點(diǎn)都是 同質(zhì)（homogeneous 的，意味著每個(gè)在歐式空間的點(diǎn)都是等價(jià)的，因此你在平移原點(diǎn)坐標(biāo)，旋轉(zhuǎn)坐標(biāo)軸的同時(shí)，其實(shí)也是在進(jìn)行著一系列的歐式變換。顯然了，歐式變換并不能改變客體的實(shí)際長(zhǎng)度，畢竟是看作剛體而研究的，同時(shí)也改變不了客體的線與線之間的角度，當(dāng)然，平行線更是不會(huì)被改變了，原來(lái)相對(duì)平行的線，經(jīng)過歐式變換后仍然還是相對(duì)平行的，如Fig 3.1所示。這個(gè)當(dāng)然不是理所當(dāng)然的，幾何變換很多是不保留這些幾何元素的，如果大家學(xué)過繪畫或者攝影，就會(huì)發(fā)現(xiàn)所謂的透視原理就是典型的一種，不過這個(gè)暫且作為后話吧。

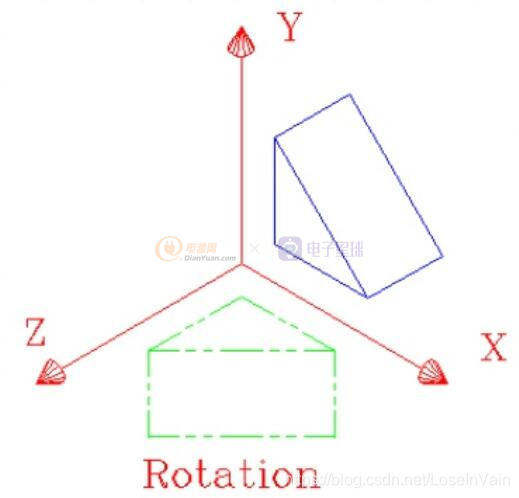
Fig 3.1 歐式變換之一的旋轉(zhuǎn)，我們發(fā)現(xiàn)，原來(lái)是直角的，變換后還是直角，原先平行的直線，轉(zhuǎn)換后還是直角。

我們對(duì)歐幾里德變換有了初步的認(rèn)識(shí)，那么歐幾里德變換是不是在研究工作中就足夠使用了呢？很遺憾，顯然不是的，比如計(jì)算機(jī)圖形學(xué)中那么多需要對(duì)圖形進(jìn)行放大，縮小的操作在歐幾里德變換中顯然是失效的。因此我們還需要定義一種變換，能使得放大，縮小能夠操作起來(lái)有理論依據(jù)。

這個(gè)其實(shí)并不困難，我們只需要在保持原點(diǎn)位置，坐標(biāo)軸的指向方向不變的情況下，將每個(gè)坐標(biāo)軸都“拉伸”或者“縮小”相同的倍數(shù)就行了，注意，是每個(gè)坐標(biāo)軸都是相同的倍數(shù)。如果結(jié)合起歐幾里德變換，那么我們就會(huì)發(fā)現(xiàn)我們可以旋轉(zhuǎn)，平移，放大縮小我們的研究客體了，我們將其稱之為相似性變換(similarity transformations)或者度量變換(metric transformations)。注意到，相似性變換包括了歐幾里德變換，即是 。

然而，有了放大縮小，我們似乎還是還缺少了一些變換工具，去描述客體在某個(gè)特定方向的單獨(dú)的拉伸或者縮小，而這在某些特殊情況下的成像中是必須的工具（見[5,6]中的仿射相機(jī)部分知識(shí)點(diǎn)）。于是我們引入了仿射變換(affine transformation)，在仿射變換中，每個(gè)軸不再是像相似性變換中一樣都是放縮同樣的倍數(shù)了，而是可能放縮不同的尺度。注意到，仿射變換包括了相似性變換和歐幾里德變換，即是 。

這樣足夠了嗎？我們成像出來(lái)的物體，在引入了仿射變換之后，也就是如果我們用仿射相機(jī)去拍攝一個(gè)正方體，會(huì)形成如Fig 3.2所示的效果的平面圖形（當(dāng)然，忽視虛線部分）。我們會(huì)發(fā)現(xiàn)，如果光從這個(gè)平面圖形，我們完全沒法推斷出這個(gè)客體在三維立體空間的深度信息，客體因?yàn)樵诳臻g中各個(gè)部分距離相機(jī)中心的距離或多或少有所不同，正如我們?cè)赱7]中的“透視投影的若干性質(zhì)”中曾經(jīng)討論過的，這種因?yàn)榭腕w深度不同本應(yīng)該導(dǎo)致投影縮放（foreshortening）在內(nèi)的投影變形，而這種變形 表現(xiàn)出來(lái)就是遠(yuǎn)小近大，在客體某些線條就算本身尺度上是一樣的，在投影的平面上都可能會(huì)產(chǎn)生一定的比例關(guān)系。 這種變形有時(shí)候正是我們想要的，對(duì)于我們?nèi)祟悘钠矫鎴D形中理解客體在立體工具的深度是不可或缺的存在。因此，如果光用仿射相機(jī)，那么形成出來(lái)的二維圖像就完全失去了推斷出客體深度的信息。（如果你的素描老師看到你畫的圖如Fig 3.2所示，大概會(huì)直接掛科吧，RIP）。

Fig 3.2 在仿射相機(jī)角度下的立方體，是沒有任何立體感的，因?yàn)槠渚€條長(zhǎng)度的比例不能體現(xiàn)因?yàn)榭腕w不同部件距離相機(jī)的距離不同而導(dǎo)致的投影變形，這種變形對(duì)于我們?nèi)祟愒谄矫嫔险J(rèn)識(shí)客體的深度信息，卻是非常關(guān)鍵的。

我們?cè)撛趺崔k？相機(jī)的初衷是在平面上對(duì)客體，對(duì)大自然進(jìn)行復(fù)刻，那么自然想要保存更多的原始信息，丟失了深度信息可完全不劃算，因此我們還需要引入一個(gè)變換形式，我們稱之為投影變換（projective transformations），注意到，投影變換包括了仿射變換，相似性變換，歐幾里德變換，也就是

因此投影變換是一個(gè)非常大的種類，其中可以解決我們剛才提到的，在二維平面上體現(xiàn)三維客體的深度信息的成像方法，稱之為透視法（perspective），學(xué)素描和攝影的讀者應(yīng)該對(duì)這個(gè)術(shù)語(yǔ)很熟悉吧。透視法的原則就是遠(yuǎn)處的物體看起來(lái)小，近處的物體看起來(lái)大，所謂的“遠(yuǎn)小近大”，在透視法中，平行線是會(huì)在無(wú)窮遠(yuǎn)處相交的，這個(gè)相交點(diǎn)可以稱之為消失點(diǎn)（vanish point），聯(lián)想到我們?cè)?jīng)定義的理想點(diǎn)的概念，我們知道消失點(diǎn)便是理想點(diǎn)。透視法呈現(xiàn)的圖像如Fig 3.3所示：

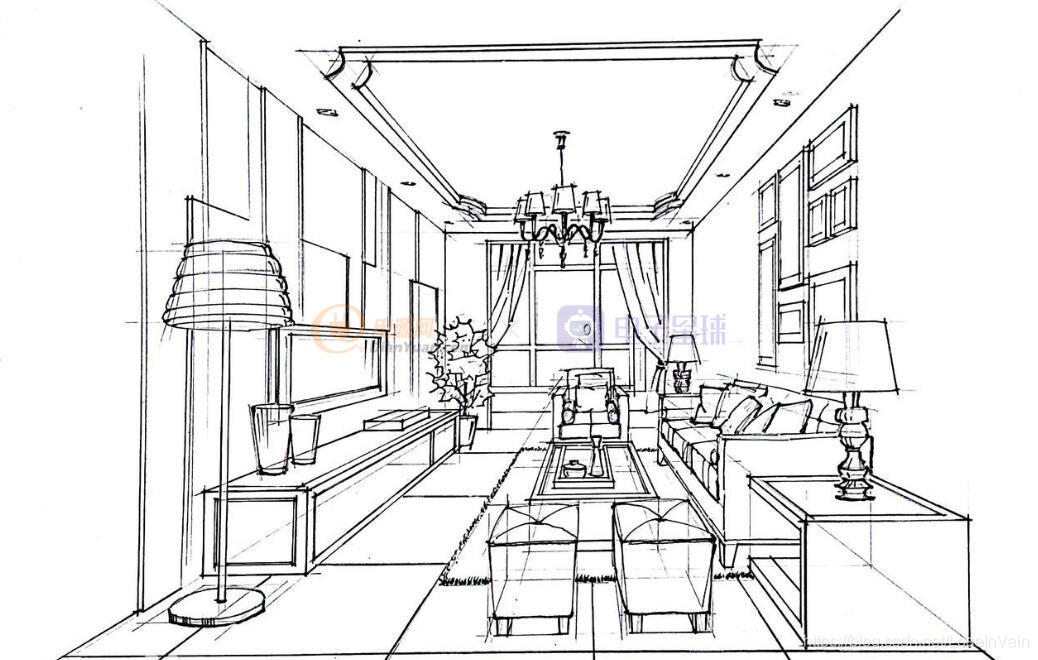
Fig 3.3 通過透視法繪畫得到的場(chǎng)景，可以通過計(jì)算線條之間的相對(duì)比例從而恢復(fù)出相對(duì)景深的大小，當(dāng)然絕對(duì)景深光從比例還是不夠的，例如你不可能知道這個(gè)椅子的絕對(duì)尺寸是多少，但是你可以推算出每個(gè)椅子之間的具體尺寸比例。

從Fig 3.3中，我們可以通過計(jì)算線條比例，從而對(duì)場(chǎng)景客體的相對(duì)景深進(jìn)行一定程度上的重建，當(dāng)然這個(gè)重建不是完美的，我們需要很多后續(xù)討論的工具才能更好地進(jìn)行重建。但是，起碼通過投影變換中的透視法，我們能夠在二維圖像上保存更多的三維客體的信息了。

這里我要插個(gè)嘴，到底什么叫做投影（projectivity）呢？我們最為直觀的印象就是太陽(yáng)光照著不可透光的房子，形成的倒影，如Fig 3.4所示。這個(gè)直觀感覺是正確的，確實(shí)我們也是這樣定義的：

投影性（projectivity）是一種映射h hh，其可以從投影幾何空間（當(dāng)然也可以是三維的，見下一章節(jié)的介紹）映射回這個(gè)投影幾何空間，使得當(dāng)且僅當(dāng)三點(diǎn)共線時(shí)，也是共線的。

因此投影線也稱之為單應(yīng)性（homography）[8]或者共線性（colineation），顯然共線性這個(gè)名稱更為形象生動(dòng)。投影性其實(shí)表示的是在投影前后，直線還是直線，該共線的點(diǎn)還是共線的，就那么簡(jiǎn)單，完事兒。不過多說(shuō)一句，這種共線性可以用矩陣形式表達(dá)，如在二維空間中(用的是齊次坐標(biāo)系)：

Fig 3.4 投影，我們的直觀印象就是太陽(yáng)光在不可透光客體上的形成的影子。

這就是我們暫時(shí)的所有變換了：歐幾里德變換，相似性變換，仿射變換和投影變換。當(dāng)然，在本章節(jié)只是從感性的角度去理解這些變換的概念，我們接下來(lái)才是正式地步入深入理解這些變換背后的數(shù)學(xué)含義的章節(jié)，讓我們繼續(xù)吧。

投影幾何空間和齊次坐標(biāo)系更配哦~是的你沒看錯(cuò)，這一章又會(huì)和齊次坐標(biāo)系扯上關(guān)系了，不過我們還是從歐幾里德幾何空間說(shuō)起吧。還記得我們的歐幾里德空間嗎，在這個(gè)空間里面的變換不管你怎么變換，無(wú)限遠(yuǎn)處的點(diǎn)永遠(yuǎn)都在無(wú)限遠(yuǎn)處，而有限的點(diǎn)永遠(yuǎn)都不可能跑到無(wú)限遠(yuǎn)處對(duì)吧，這個(gè)是顯而易見的。這個(gè)性質(zhì)同樣在相似幾何空間，仿射幾何空間成立，有限遠(yuǎn)的就是有限遠(yuǎn)的，無(wú)限遠(yuǎn)的就是無(wú)限遠(yuǎn)的，各自為政，誰(shuí)也不干擾誰(shuí)。因此在這些空間去描述變換，實(shí)際上并不需要齊次坐標(biāo)系，只需要非齊次坐標(biāo)系就足夠了，因?yàn)槲覀兏揪筒恍枰ッ枋隼硐朦c(diǎn)。

但是，我們還有個(gè)投影幾何空間，而在這個(gè)空間里面，幾何變換是很“任性”的，變換前后平行性是得不到保證的，為什么呢？因?yàn)檎菦]辦法保證平行性，我們才能提供視覺上的深度信息，這個(gè)正是我們想要的。平行性得不到保證，意味著變換前是平行的線，我們知道其交點(diǎn)在理想點(diǎn)處，變化后就可能不再平行了，那么其交點(diǎn)就變成了在有限遠(yuǎn)處的一個(gè)點(diǎn)了，反過來(lái)也是成立的。這個(gè)在非齊次坐標(biāo)系下根本沒辦法解決，畢竟非齊次坐標(biāo)連理想點(diǎn)和理想線，理想面都沒辦法描述，又怎么能描述其變換過程呢？因此我們正式引入齊次坐標(biāo)系，在投影幾何空間中，我們必須使用齊次坐標(biāo)系描述變換過程，為了四個(gè)種類變換的公式表達(dá)的形式上的統(tǒng)一，我們對(duì)于這四種幾何空間的變換，一致性地采用齊次坐標(biāo)系。

那么假設(shè)歐幾里德空間用表示，為了體現(xiàn)投影幾何空間的特殊性，我們干脆給他一個(gè)表示吧，就表示為，順便我們也給仿射空間一個(gè)表示。（別傷心啦，你其實(shí)不是順便的，后面我們還用得上呢，嘿嘿）。

數(shù)學(xué)形式的四大類型幾何變換在用數(shù)學(xué)形式描述四大類型的幾何變換之前，我們要先探討下，到底什么叫“幾何變換”？幾何變換不應(yīng)該只是幾個(gè)公式咻咻咻地套進(jìn)去，然后從一堆數(shù)字到另一堆數(shù)字的過程，幾何變換的過程中，我們要留意的是，到底什么幾何元素一直沒有改變，而什么幾何元素可能會(huì)改變的。這種變換前后的不變性，對(duì)于研究幾何變換來(lái)說(shuō)是很重要的，變換的不變性在計(jì)算機(jī)視覺中也會(huì)提供很重要的點(diǎn)子，是一個(gè)不可忽視的要點(diǎn)。不管怎么說(shuō)，我們接下來(lái)要留意幾何變換的不變性了。注意，接下來(lái)的討論都在三維空間的例子中討論，涉及到二維空間時(shí)將會(huì)特別提醒。

投影變換因?yàn)橥队白儞Q的范圍是最廣的，其數(shù)學(xué)形式是最為通用的，于是我們就先從投影變換開始討論吧。正如式子(3.1)所展示的，我們可以通過線性矩陣變換來(lái)描述投影變換，如：

注意到其實(shí)自由度是15，雖然他有16個(gè)元素，具體原因見[4]中的關(guān)于自由度的說(shuō)明。在投影變換中，只有共線性，切線性和交叉比(cross-ratio)是不變的。共線性我們之前說(shuō)過了，切線性指的是，在變換前某個(gè)直線是某個(gè)曲線的切線，那么變換后這個(gè)性質(zhì)同樣保留。投影變換不保留平行性，也不保留無(wú)限遠(yuǎn)處的理想點(diǎn)的位置，因此變換前后，無(wú)限可能變成有限，反之亦然。

至于交叉比，我們這樣理解，假設(shè)客體上有四個(gè)點(diǎn)共線，分別是，那么在選定了參考點(diǎn)之后，其他的共線的點(diǎn)可以被如下式子統(tǒng)一表示：

那么交叉比表示為：

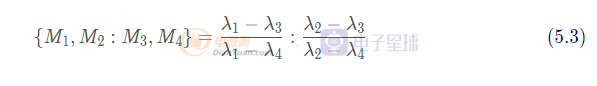
這個(gè)交叉比的具體比例和參考點(diǎn)的選定無(wú)關(guān)，并且其在投影變換下保持不變。這個(gè)性質(zhì)為我們通過平面的幾何體線條比例去計(jì)算客體的相對(duì)深度信息提供了依據(jù)。

如圖Fig 5.1所示，這個(gè)是一個(gè)特殊的投影變換——透視法后的一個(gè)正方體的二維透視圖。我們發(fā)現(xiàn)平行線相交于理想點(diǎn)? 。

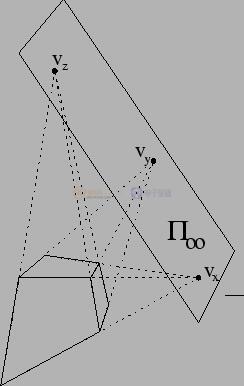
Fig 5.1 透視法下的正方體二維圖形。具體的一些消失點(diǎn)的計(jì)算，可以參考我以前的博客[9]，這里不贅述。

仿射變換

仿射變換的數(shù)學(xué)形式如(5.4)(5.5)所示，可以發(fā)現(xiàn)是對(duì)投影變換進(jìn)行了一些元素上的約束后產(chǎn)生的，一般常見的仿射變換子類型包括旋轉(zhuǎn)（rotation），尺度放縮（scale），平移（translation），切變（shear），具體的公式和約束條件見以前的博文[3]。注意到仿射變換前后的不變性繼承了投影變換的不變性，也即是共線性，交叉比和切線性。

其的約束是：

容易發(fā)現(xiàn)的是，仿射變換的自由度是12，并且容易可以驗(yàn)證仿射變換不會(huì)移動(dòng)無(wú)限遠(yuǎn)處的理想面，可以簡(jiǎn)單證明下：

在仿射變換后，理想面變成

我們從(2.2)知道了對(duì)于理想面的表達(dá)為。于是容易驗(yàn)證 因此未曾改變理想面。然而，在理想面上的理想點(diǎn)的位置即便沒有從無(wú)限遠(yuǎn)處變成有限遠(yuǎn)處，在仿射變換下也可能在理想面上發(fā)生偏移，也就是說(shuō)仿射變換不保留理想面上點(diǎn)的位置。這一點(diǎn)可以簡(jiǎn)單證明下，假設(shè)理想面上有一個(gè)圓錐線[4] 其中單位矩陣，假設(shè)仿射變換后有點(diǎn)的位置偏移，那么我們可以知道，變換后的

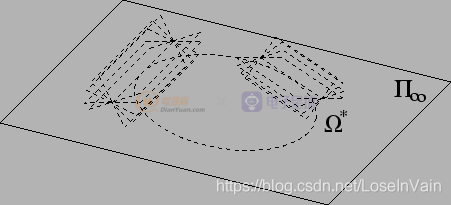
Fig 5.2 在理想面上有一個(gè)圓錐線，仿射變換前后圓錐線軌跡可能會(huì)改變。

注意到在沒有其他約束的情況下，此圓錐線軌跡已經(jīng)變了。其實(shí)這一點(diǎn)也很容易理解，我們對(duì)仿射幾何空間的坐標(biāo)軸進(jìn)行拉伸收縮，每一個(gè)軸進(jìn)行的幅度是不同的，因此在理想面上的圓錐線自然會(huì)發(fā)生拉伸形變，比如說(shuō)，可能會(huì)從圓形變成橢圓形。（事實(shí)上，圓錐曲線在投影變換下等價(jià)，這點(diǎn)也容易證明，暫且忽略）。

至于仿射變換的平行性不變性，這點(diǎn)非常容易證明，就留個(gè)讀者證明吧。

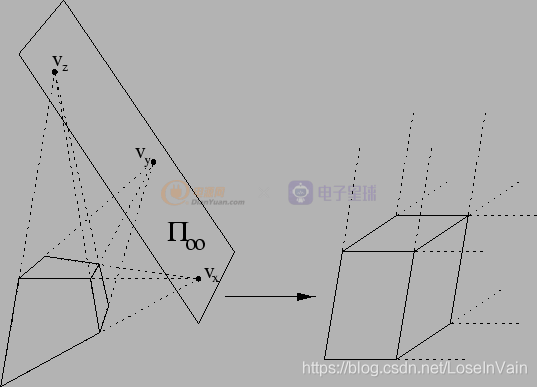
Fig 5.3 這里闡述了描述一個(gè)正方體，在投影幾何空間和仿射幾何空間中的表示方式。

相似性變換

正如我們之前所說(shuō)的，相似性變換是在歐幾里德空間的每個(gè)坐標(biāo)軸都拉伸收縮相同的幅度產(chǎn)生的，那么自然地，理想面上的圓錐曲線形狀是不會(huì)改變的，至于這個(gè)圓錐曲線變得“多大多小”，這種尺度小大的是不影響不變性的。相似性變換的公式如：

其中，注意到存在一些約束：

也就是說(shuō)的子矩陣是一個(gè)正交矩陣，并且其行列式值為1（可以視為進(jìn)行過歸一化）。事實(shí)上，這里的可以視為是旋轉(zhuǎn)矩陣，而可以視為是將變換前的原點(diǎn)坐標(biāo)挪到該處，是一個(gè)平移偏置向量。而表示的正是對(duì)整個(gè)客體的放縮尺寸大小。于是我們發(fā)現(xiàn)，整個(gè)的自由度為7，其中3個(gè)是朝向相關(guān)的自由度，3個(gè)是平移相關(guān)的，而1個(gè)是尺度大小相關(guān)的。

考慮到相似性變換前后的不變性，除了繼承了仿射變換的不變性之外，還添加了兩個(gè)重要的新的不變性：**相對(duì)距離不變 **和 角度不變。相對(duì)距離不變指的是變換前后每個(gè)線條的比例是一定的，線條之間的距離的比例也是不變的；角度不變就很好理解了，變換前后，線條之間的夾角不變。

對(duì)比仿射變換，相似性變換的理想面的圓錐線有個(gè)非常重要的性質(zhì)，其變換前后形狀不變。我們可以嘗試對(duì)此進(jìn)行證明。正如Fig 5.2所示，我們假設(shè)理想面?  上的二次曲錐面為， 但是二次曲錐面是一個(gè)立體圖形，不容易可視化，我們經(jīng)常用其對(duì)偶二次曲錐面為表示，其表現(xiàn)為一系列的平面。理想面上的二次曲錐面稱之為絕對(duì)二次曲錐面（Absolute Quadric）。

二次曲錐面是在三維情況下的，在平面上的情況，二次曲錐面就變成了圓錐線? ，其對(duì)偶形式為一系列的直線，表示為。我們將理想面上的圓錐線稱之為絕對(duì)圓錐線（Image of Absolute Conic， IAC）。

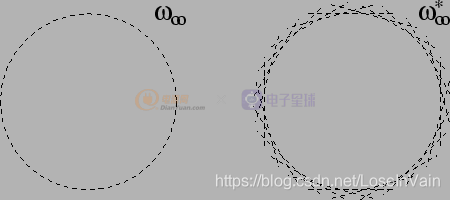
Fig 5.4 理想面上的絕對(duì)圓錐線和其對(duì)偶形式

我們暫且只考慮三維情況下的，其最簡(jiǎn)單的形式就是一個(gè)球：

其矩陣形式為：

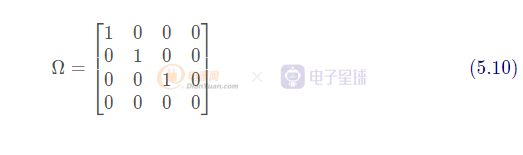
二次曲錐面的方程是，經(jīng)過相似性變換后，。于是變換后，新的二次曲錐面可以表示為：

為了方便，我們將用分塊矩陣的方式計(jì)算這個(gè)矩陣：

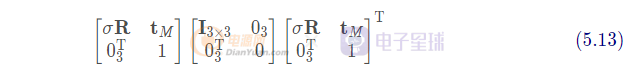
于是有：

因?yàn)?span>是尺度因子，因此對(duì)形狀沒有影響，我們發(fā)現(xiàn)變換前后絕對(duì)圓錐線的形狀不變。

Fig 5.5 左圖是仿射變換，右圖是相似性變換的結(jié)果。

歐幾里德變換歐幾里德變換在相似性變換的基礎(chǔ)上，只是把尺度因子設(shè)置為了1， 其他不變，因此在繼承了相似性變換的所有不變性特性的基礎(chǔ)上，又增加了絕對(duì)長(zhǎng)度不變性。我們有：

因此其自由度就只剩下了3個(gè)方向自由度，3個(gè)平移自由度。

總結(jié)

洋洋灑灑地寫了一大堆，現(xiàn)在總結(jié)下這四大變換的自由度和不變性：

投影變換，自由度15，不變性：交叉比，共線性，切線性。

仿射變換，自由度12，不變性：交叉比，共線性，切線性， 軸方向的相對(duì)距離不變，平行不變，理想面不變。

相似性變換，自由度7，不變性：交叉比，共線性，切線性， 軸方向的相對(duì)距離不變，平行不變，理想面不變， 相對(duì)距離不變，角度不變，絕對(duì)圓錐線不變。

歐幾里德變換，自由度6，不變性：交叉比，共線性，切線性， 軸方向的相對(duì)距離不變，平行不變，理想面不變，相對(duì)距離不變，角度不變，絕對(duì)圓錐線不變，絕對(duì)距離不變。

PS: 本文引出絕對(duì)圓錐線的概念，是為了以后的立體視覺中的恢復(fù)重建任務(wù)和相機(jī)參數(shù)標(biāo)定等任務(wù)進(jìn)行鋪墊。

Reference

[1]. Hartley R, Zisserman A. Multiple View Geometry in Computer Vision[J]. Kybernetes, 2008, 30(9/10):1865 - 1872.

[2]. https://www.cs.unc.edu/~marc/tutorial/node3.html

[3]. https://blog.csdn.net/LoseInVain/article/details/102756630

[4]. https://blog.csdn.net/LoseInVain/article/details/104515839

[5]. https://blog.csdn.net/LoseInVain/article/details/102869987

[6]. https://blog.csdn.net/LoseInVain/article/details/102883243

[7]. https://blog.csdn.net/LoseInVain/article/details/102698703

[8]. https://blog.csdn.net/LoseInVain/article/details/102739778

[9].https://blog.csdn.net/LoseInVain/article/details/102756630