數據結構是什么?
程序 = 數據結構 + 算法
是的,上面這句話是非常經典的,程序由數據結構以及算法組成,當然數據結構和算法也是相輔相成的,不能完全獨立來看待,但是本文會相對重點聊聊那些常用的數據結構。
數據結構是什么呢?
首先得知道數據是什么?數據是對客觀事務的符號表示,在計算機科學中是指所有能輸入到計算機中并被計算機程序處理的符號總稱。那為何加上“結構”兩字?
數據元素是數據的基本單位,而任何問題中,數據元素都不是獨立存在的,它們之間總是存在著某種關系,這種數據元素之間的關系我們稱之為結構。
因此,我們有了以下定義:
數據結構是計算機存儲、組織數據的方式。數據結構是指相互之間存在一種或多種特定關系的數據元素的集合。通常情況下,精心選擇的數據結構可以帶來更高的運行或者存儲效率。數據結構往往同高效的檢索算法和索引技術有關。
簡單講,數據結構就是組織,管理以及存儲數據的方式。雖然理論上所有的數據都可以混雜,或者混合,或者饑不擇食,隨便存儲,但是計算機是追求高效的,如果我們能了解數據結構,找到較為適合當前問題場景的數據結構,將數據之間的關系表現在存儲上,計算的時候可以較為高效的利用適配的算法,那么程序的運行效率肯定也會有所提高。
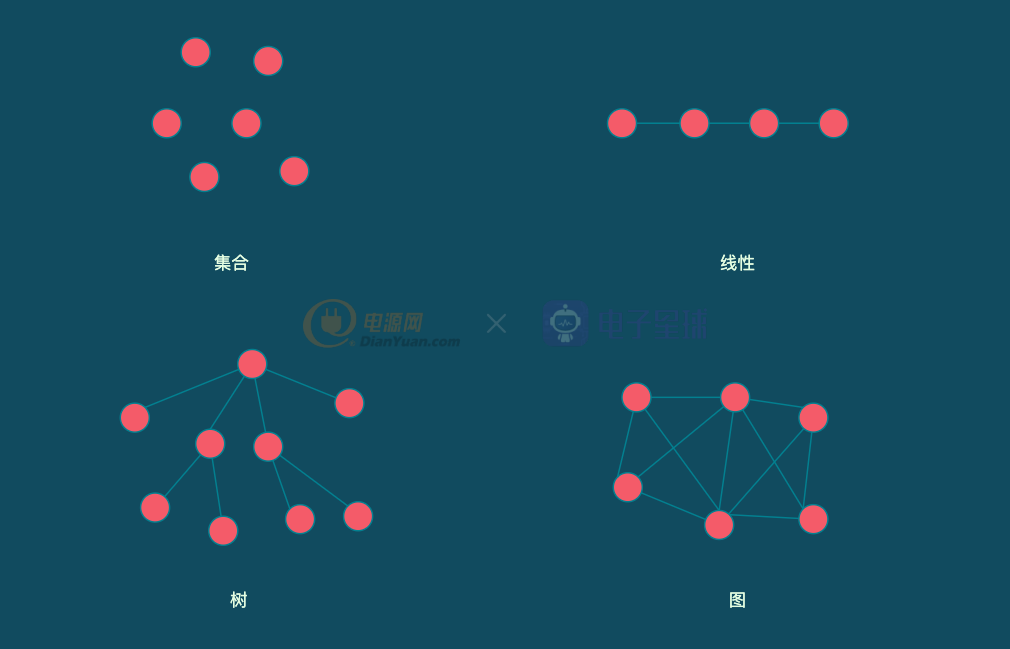
常用的4種數據結構有:
- 集合:只有同屬于一個集合的關系,沒有其他關系
- 線性結構:結構中的數據元素之間存在一個對一個的關系
- 樹形結構:結構中的數據元素之間存在一個對多個的關系
- 圖狀結構或者網狀結構:圖狀結構或者網狀結構
何為邏輯結構和存儲結構?
數據元素之間的邏輯關系,稱之為邏輯結構,也就是我們定義了對操作對象的一種數學描述。但是我們還必須知道在計算機中如何表示它。數據結構在計算機中的表示(又稱為映像),稱之為數據的物理結構,又稱存儲結構。
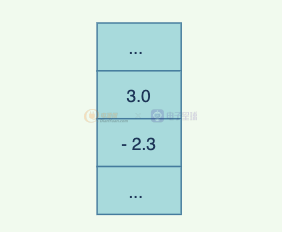
數據元素之前的關系在計算機中有兩種不同的表示方法:順序映像和非順序映像,并且由此得到兩種不同的存儲結構:順序存儲結構和鏈式存儲結構,比如順序存儲結構,我們要表示復數z1 =3.0 - 2.3i ,可以直接借助元素在存儲器中的相對位置來表示數據元素之間的邏輯關系:
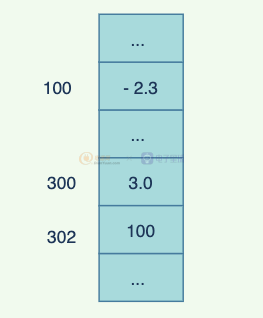
而鏈式結構,則是以指針表示數據元素之間的邏輯關系,同樣是z1 =3.0 - 2.3i ,先找到下一個是 100,是一個地址,根據地址找到真實的數據-2.3i:
位(bit)
在計算機中表示信息的最小的單位是二進制數中的一位,叫做位。也就是我們常見的類似01010101010這種數據,計算機的底層就是各種晶體管,電路板,所以不管是什么數據,即使是圖片,聲音,在最底層也是0和1,如果有八條電路,那么每條電路有自己的閉合狀態,有8個2相乘,28,也就是256種不同的信號。
但是一般我們需要表示負數,也就是最高的一位表示符號位,0表示正數,1表示負數,也就是8位的最大值是01111111,也就是127。
值得我們注意的是,計算機的世界里,多了原碼,反碼,補碼的概念:
- 源碼:用第一位表示符號,其余位表示值
- 反碼:正數的補碼反碼是其本身,負數的反碼是符號位保持不變,其余位取反。
- 補碼:正數的補碼是其本身,負數的補碼是在其反碼的基礎上 + 1
為什么有了原碼還要反碼和補碼?
我們知道加減法是高頻的運算,人可以很直觀地看出加號減號,馬上就可以算出來,但是計算機如果區分不同的符號,那么加減就會比較復雜,比如正數+正數,正數-正數,正數-負數,負數+負數...等等。于是,有人就想用同一個運算器(加號運算器),解決所有的加減法計算,可以減少很多復雜的電路,以及各種符號轉換的開銷,計算也更加高效。
我們可以看到,下面負數參加運算的結果也是符合補碼的規則的:
00100011 35
+ 11011101 -35
-------------------------
00000000 0
00100011 35
+ 11011011 -37
-------------------------
11111110 -2
當然,如果計算結果超出了位數所能表示的范圍,那就是溢出,就說明需要更多的位數才能正確表示。
一般能用位運算的,都盡量使用位運算,因為它比較高效, 常見地位置運算:
- ~:按位取反
- &:按為與運算
- |:按位或運算
- ^:按位異或
- <<: 帶符號左移,比如35(00100011),左移一位為 70(01000110),-35(11011101)左移一位為-70(10111010)
- >>:帶符號右移,比如35(00100011),右移一位為 17(00010001),-35(11011101)左移一位為-18(11101110)
- <<<:無符號左移,比如35(00100011),左移一位為70(01000110)
- >>>:無符號右移,比如-35(11011101),右移一位為110(01101110)
- x ^= y; y ^= x; x ^= y;:交換
- s &= ~(1 << k):第k位置0
要說哪里使用位運算比較經典,那么要數布隆過濾器,需要了解詳情的可以參考:http://aphysia.cn/archives/cachebloomfilter
布隆過濾器是什么呢?
布隆過濾器(Bloom Filter)是由布隆(Burton Howard Bloom)在1970年提出的,它實際上是由一個很長的二進制向量和一系列隨機hash映射函數組成(說白了,就是用二進制數組存儲數據的特征)。可以使用它來判斷一個元素是否存在于集合中,它的優點在于查詢效率高,空間小,缺點是存在一定的誤差,以及我們想要剔除元素的時候,可能會相互影響。
也就是當一個元素被加入集合的時候,通過多個hash函數,將元素映射到位數組中的k個點,置為1。
重點是多個hash函數,可以將數據hash到不同地位上,也只有這些位全部為1的時候,我們才能判斷該數據已經存在
假設有三個hash函數,那么不同的元素,都會使用三個hash函數,hash到三個位置上。
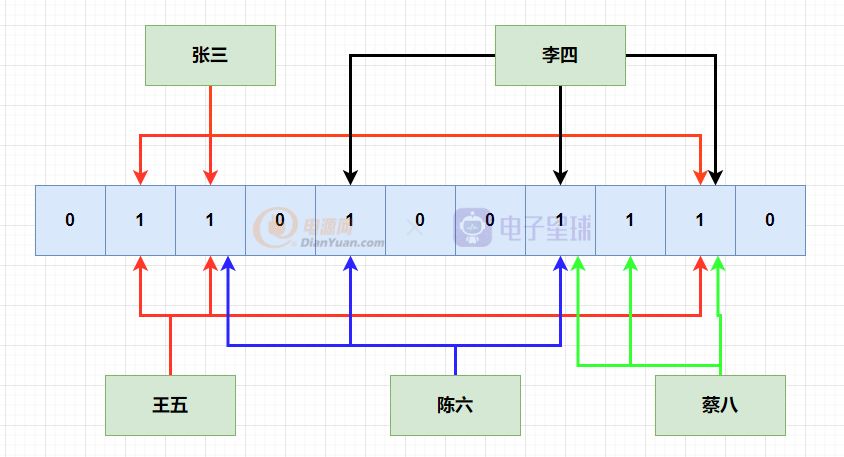
假設后面又來了一個張三,那么在hash的時候,同樣會hash到以下位置,所有位都是1,我們就可以說張三已經存在在里面了。

那么有沒有可能出現誤判的情況呢?這是有可能的,比如現在只有張三,李四,王五,蔡八,hash映射值如下:
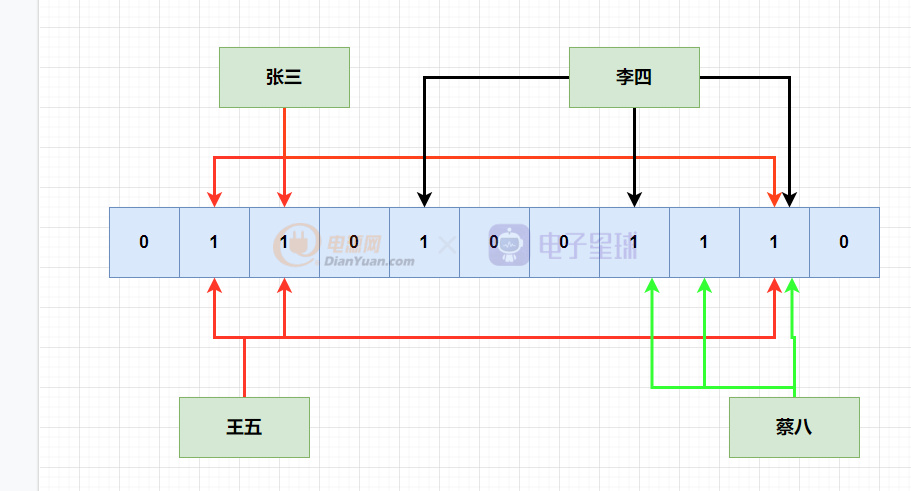
后面來了陳六,但是不湊巧的是,它hash的三個函數hash出來的位,剛剛好就是被別的元素hash之后,改成1了,判斷它已經存在了,但是實際上,陳六之前是不存在的。
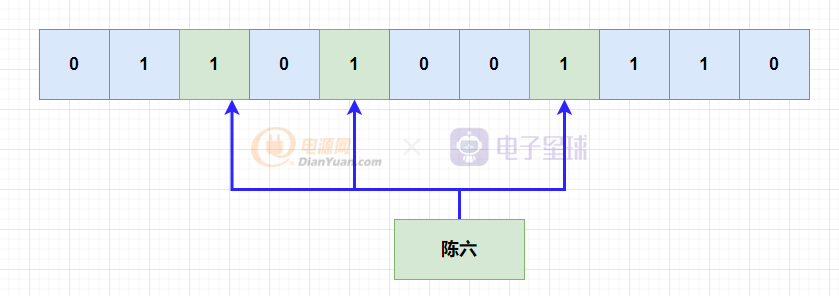
上面的情況,就是誤判,布隆過濾器都會不可避免地出現誤判。但是它有一個好處是,布隆過濾器,判斷存在的元素,可能不存在,但是判斷不存在的元素,一定不存在。,因為判斷不存在說明至少有一位hash出來是對不上的。
也是由于會出現多個元素可能hash到一起,但有一個數據被踢出了集合,我們想把它映射地位,置為0,相當于刪除該數據。這個時候,就會影響到其他的元素,可能會把別的元素映射地位置,置為了0。這也就是為什么布隆過濾器不能刪除的原因。
數組
線性表示最常用而且最為簡單的一種數據結構,一個線性表示 n 數據元素的有限序列,有以下特點:
- 存在唯一的第一個數據元素
- 存在唯一被稱為最后一個的數據元素
- 除了第一個以外,集合中每一個元素均有一個前驅
- 除了最后一個元素之外,集合中的每一個數據元素都有一個后繼元素
線性表包括下面幾種:
- 數組:查詢 / 更新快,查找/刪除慢
- 鏈表
- 隊列
- 棧
數組是線性表的一種,線性表的順序表示指的是用一組地址連續的存儲單元依次存儲線性表的數據元素:
在Java中表示為:
int[] nums = new int[100];
int[] nums = {1,2,3,4,5};
Object[] Objects = new Object[100];
在C++ 中表示為:
int nums[100];
數組是一種線性的結構,一般在底層是連續的空間,存儲相同類型的數據,由于連續緊湊結構以及天然索引支持,查詢數據效率高:
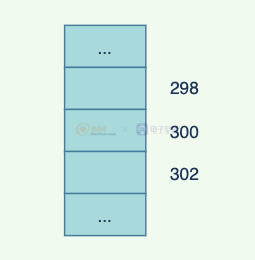
假設我們知道數組a的第 1 個值是 地址是 296,里面的數據類型占 2 個 單位,那么我們如果期望得到第 5 個: 296+(5-1)*2 = 304,O(1)的時間復雜度就可以獲取到。
更新的本質也是查找,先查找到該元素,就可以動手更新了:
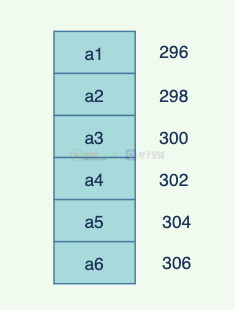
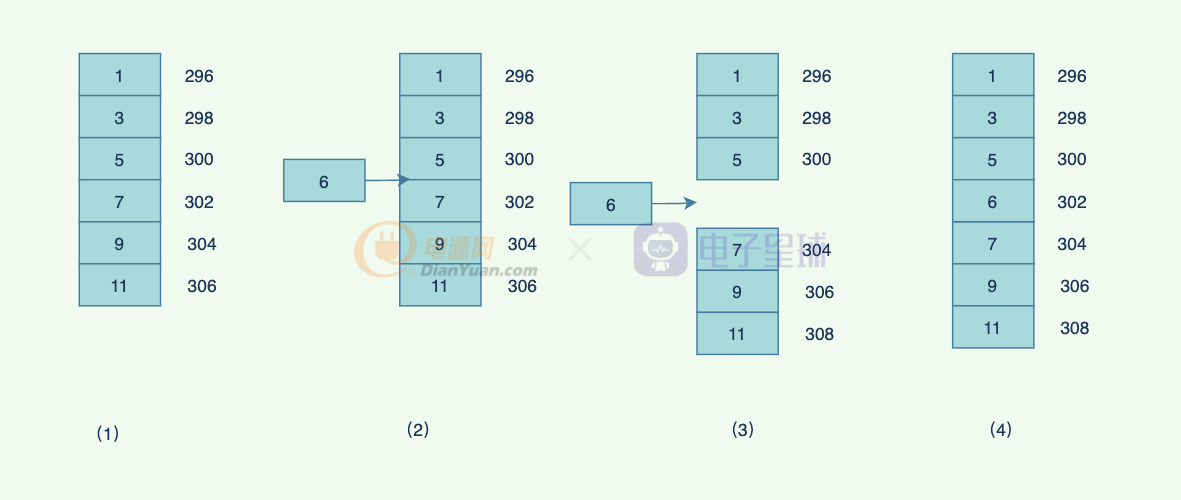
但是如果期望插入數據的話,需要移動后面的數據,比如下面的數組,插入元素6,最差的是移動所有的元素,時間復雜度為O(n)
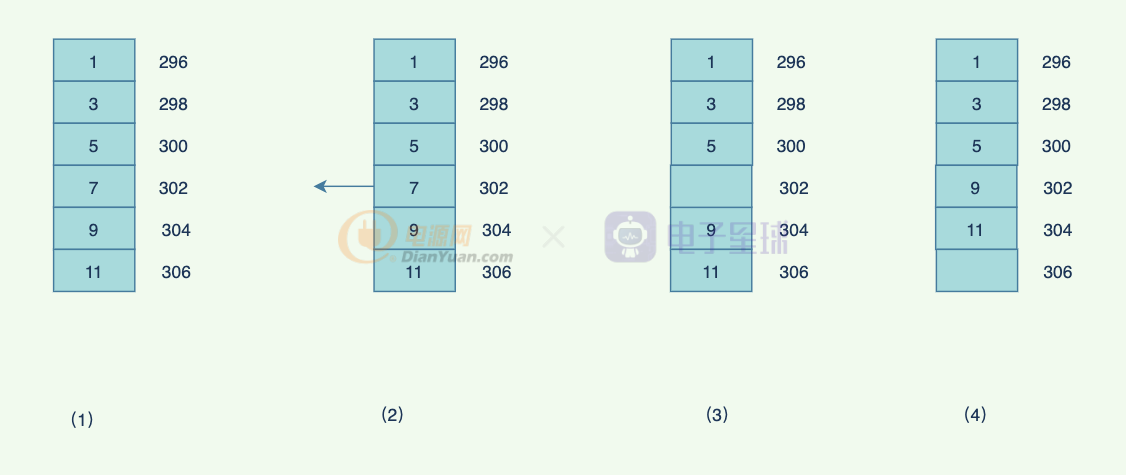
而刪除元素則需要把后面的數據移動到前面,最差的時間復雜度同樣為O(n):
Java代碼實現數組的增刪改查:
package datastruction;
import java.util.Arrays;
public class MyArray {
private int[] data;
private int elementCount;
private int length;
public MyArray(int max) {
length = max;
data = new int[max];
elementCount = 0;
}
public void add(int value) {
if (elementCount == length) {
length = 2 * length;
data = Arrays.copyOf(data, length);
}
data[elementCount] = value;
elementCount++;
}
public int find(int searchKey) {
int i;
for (i = 0; i < elementCount; i++) {
if (data[i] == searchKey)
break;
}
if (i == elementCount) {
return -1;
}
return i;
}
public boolean delete(int value) {
int i = find(value);
if (i == -1) {
return false;
}
for (int j = i; j < elementCount - 1; j++) {
data[j] = data[j + 1];
}
elementCount--;
return true;
}
public boolean update(int oldValue, int newValue) {
int i = find(oldValue);
if (i == -1) {
return false;
}
data[i] = newValue;
return true;
}
}
// 測試類
public class Test {
public static void main(String[] args) {
MyArray myArray = new MyArray(2);
myArray.add(1);
myArray.add(2);
myArray.add(3);
myArray.delete(2);
System.out.println(myArray);
}
}
鏈表
上面的例子中,我們可以看到數組是需要連續的空間,這里面如果空間大小只有 2,放到第 3 個元素的時候,就不得不擴容,不僅如此,還得拷貝元素。一些刪除,插入操作會引起較多的數據移動的操作。
鏈表,也就是鏈式數據結構,由于它不要求邏輯上相鄰的數據元素在物理位置上也相鄰,所以它沒有順序存儲結構所具有的缺點,但是同時也失去了通過索引下標直接查找元素的優點。
重點:鏈表在計算機的存儲中不是連續的,而是前一個節點存儲了后一個節點的指針(地址),通過地址找到后一個節點。
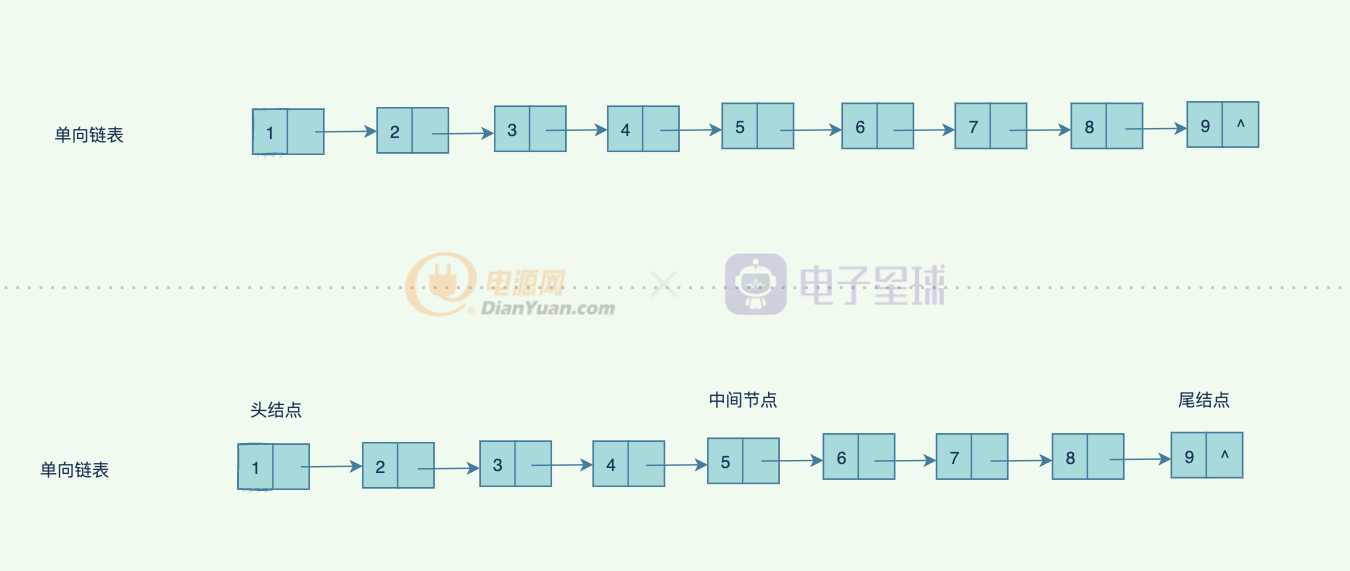
下面是單鏈表的結構:
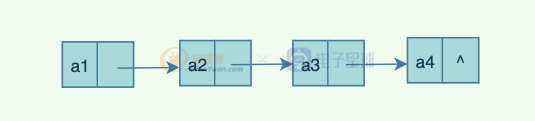
一般我們會手動在單鏈表的前面設置一個前置結點,也可以稱為頭結點,但是這并非絕對:

一般鏈表結構分為以下幾種:
- 單向鏈表:鏈表中的每一個結點,都有且只有一個指針指向下一個結點,并且最后一個節點指向空。
- 雙向鏈表:每個節點都有兩個指針(為方便,我們稱之為前指針,后指針),分別指向上一個節點和下一個節點,第一個節點的前指針指向NULL,最后一個節點的后指針指向NULL
- 循環鏈表:每一個節點的指針指向下一個節點,并且最后一個節點的指針指向第一個節點(雖然是循環鏈表,但是必要的時候還需要標識頭結點或者尾節點,避免死循環)
- 復雜鏈表:每一個鏈表有一個后指針,指向下一個節點,同時有一個隨機指針,指向任意一個結點。
鏈表操作的時間復雜度:
- 查詢:O(n),需要遍歷鏈表
- 插入:O(1),修改前后指針即可
- 刪除:O(1),同樣是修改前后指針即可
- 修改:不需要查詢則為O(1),需要查詢則為O(n)
鏈表的結構代碼怎么表示呢?
下面只表示單鏈表結構,C++表示:
// 結點
typedef struct LNode{
// 數據
ElemType data;
// 下一個節點的指針
struct LNode *next;
}*Link,*Position;
// 鏈表
typedef struct{
// 頭結點,尾節點
Link head,tail;
// 長度
int len;
}LinkList;
Java 代碼表示:
public class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
自己實現簡單鏈表,實現增刪改查功能:
class ListNode<T> {
T val;
ListNode next = null;
ListNode(T val) {
this.val = val;
}
}
public class MyList<T> {
private ListNode<T> head;
private ListNode<T> tail;
private int size;
public MyList() {
this.head = null;
this.tail = null;
this.size = 0;
}
public void add(T element) {
add(size, element);
}
public void add(int index, T element) {
if (index < 0 || index > size) {
throw new IndexOutOfBoundsException("超出鏈表長度范圍");
}
ListNode current = new ListNode(element);
if (index == 0) {
if (head == null) {
head = current;
tail = current;
} else {
current.next = head;
head = current;
}
} else if (index == size) {
tail.next = current;
tail = current;
} else {
ListNode preNode = get(index - 1);
current.next = preNode.next;
preNode.next = current;
}
size++;
}
public ListNode get(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException("超出鏈表長度");
}
ListNode temp = head;
for (int i = 0; i < index; i++) {
temp = temp.next;
}
return temp;
}
public ListNode delete(int index) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException("超出鏈表節點范圍");
}
ListNode node = null;
if (index == 0) {
node = head;
head = head.next;
} else if (index == size - 1) {
ListNode preNode = get(index - 1);
node = tail;
preNode.next = null;
tail = preNode;
} else {
ListNode pre = get(index - 1);
pre.next = pre.next.next;
node = pre.next;
}
size--;
return node;
}
public void update(int index, T element) {
if (index < 0 || index >= size) {
throw new IndexOutOfBoundsException("超出鏈表節點范圍");
}
ListNode node = get(index);
node.val = element;
}
public void display() {
ListNode temp = head;
while (temp != null) {
System.out.print(temp.val + " -> ");
temp = temp.next;
}
System.out.println("");
}
}
測試代碼如下:
public class Test {
public static void main(String[] args) {
MyList myList = new MyList();
myList.add(1);
myList.add(2);
// 1->2
myList.display();
// 1
System.out.println(myList.get(0).val);
myList.update(1,3);
// 1->3
myList.display();
myList.add(4);
// 1->3->4
myList.display();
myList.delete(1);
// 1->4
myList.display();
}
}
輸出結果:
1 -> 2 ->
1
1 -> 3 ->
1 -> 3 -> 4 ->
1 -> 4 ->
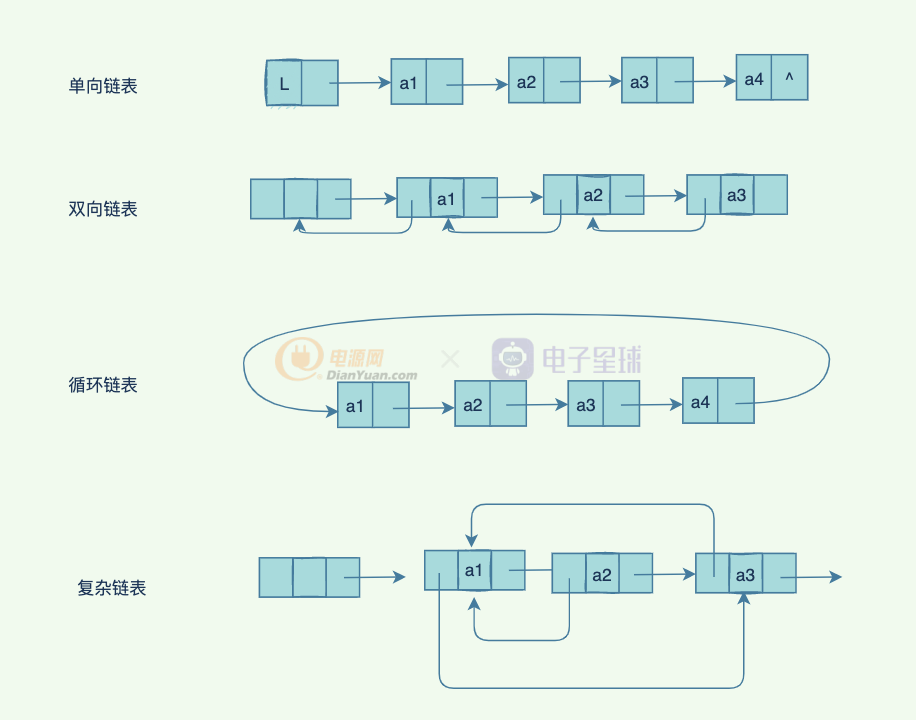
單向鏈表的查找更新比較簡單,我們看看插入新節點的具體過程(這里只展示中間位置的插入,頭尾插入比較簡單):
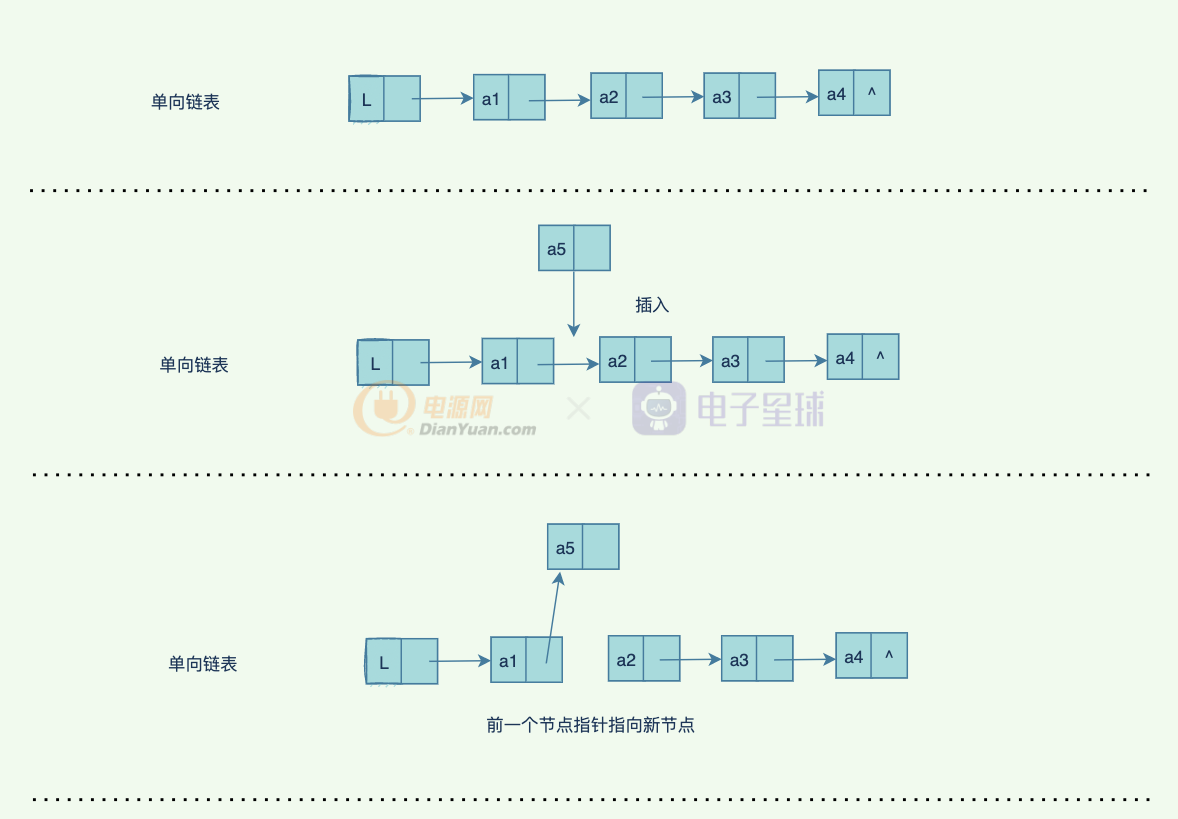
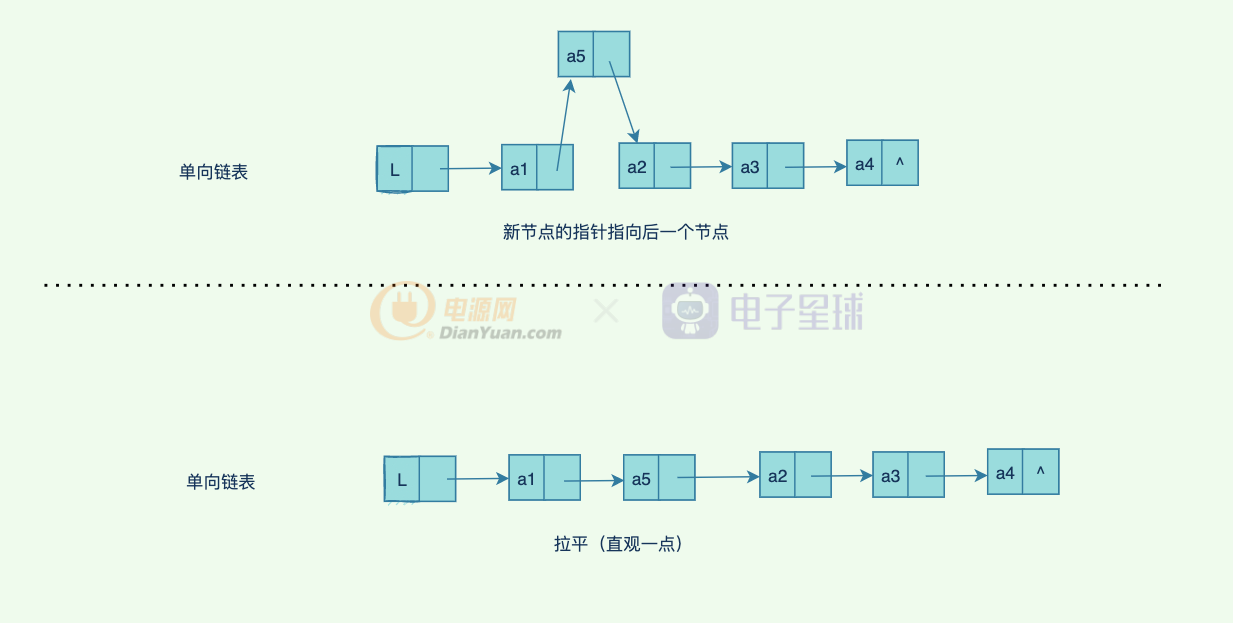
那如何刪除一個中間的節點呢?下面是具體的過程:
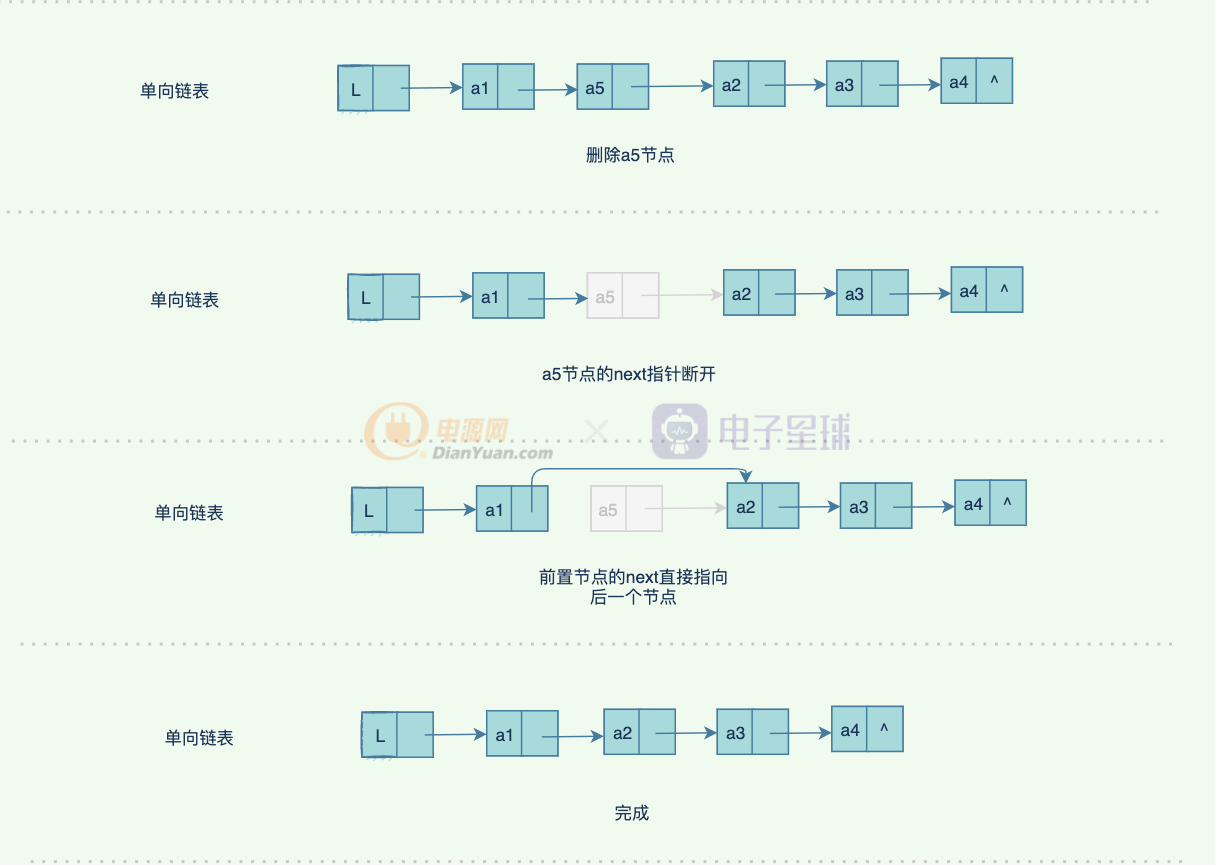
或許你會好奇,a5節點只是指針沒有了,那它去哪里了?
如果是Java程序,垃圾回收器會收集這種沒有被引用的節點,幫我們回收掉了這部分內存,但是為了加快垃圾回收的速度,一般不需要的節點我們需要置空,比如 node = null, 如果在C++ 程序中,那么就需要手動回收了,否則容易造成內存泄漏等問題。
復雜鏈表的操作暫時講到這里,后面我會單獨把鏈表這一塊的數據結構以及常用算法單獨分享一下,本文章主要講數據結構全貌。
跳表
上面我們可以觀察到,鏈表如果搜索,是很麻煩的,如果這個節點在最后,需要遍歷所有的節點,才能找到,查找效率實在太低,有沒有什么好的辦法呢?
辦法總比問題多,但是想要絕對的”多快好省“是不存在的,有舍有得,計算機的世界里,充滿哲學的味道。既然搜索效率有問題,那么我們不如給鏈表排個序。排序后的鏈表,還是只能知道頭尾節點,知道中間的范圍,但是要找到中間的節點,還是得走遍歷的老路。如果我們把中間節點存儲起來呢?存起來,確實我們就知道數據在前一半,還是在后一半。比如找7,肯定就從中間節點開始找。如果查找4,就得從頭開始找,最差到中間節點,就停止查找。
但是如此,還是沒有徹底解決問題,因為鏈表很長的情況,只能通過前后兩部分查找。不如回到原則:空間和時間,我們選擇時間,那就要舍棄一部分空間,我們每個節點再加一個指針,現在有 2 層指針(注意:節點只有一份,都是同一個節點,只是為了好看,弄了兩份,實際上是同一個節點,有兩個指針,比如 1 ,既指向2,也指向5):

兩層指針,問題依然存在,那就不斷加層,比如每兩個節點,就加一層:
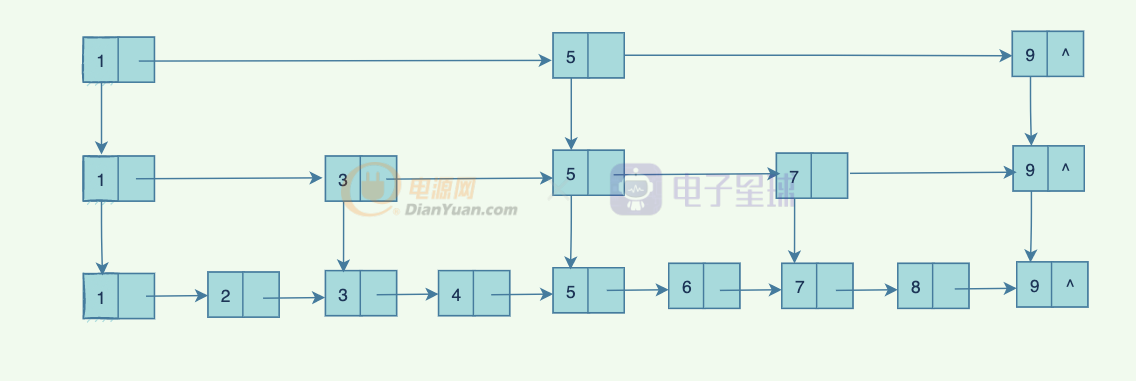
這就是跳表了,跳表的定義如下:
跳表(SkipList,全稱跳躍表)是用于有序元素序列快速搜索查找的一個數據結構,跳表是一個隨機化的數據結構,實質就是一種可以進行二分查找的有序鏈表。跳表在原有的有序鏈表上面增加了多級索引,通過索引來實現快速查找。跳表不僅能提高搜索性能,同時也可以提高插入和刪除操作的性能。它在性能上和紅黑樹,AVL樹不相上下,但是跳表的原理非常簡單,實現也比紅黑樹簡單很多。
主要的原理是用空間換時間,可以實現近乎二分查找的效率,實際上消耗的空間,假設每兩個加一層, 1 + 2 + 4 + ... + n = 2n-1,多出了差不多一倍的空間。你看它像不像書的目錄,一級目錄,二級,三級 ...

如果我們不斷往跳表中插入數據,可能出現某一段節點會特別多的情況,這個時候就需要動態更新索引,除了插入數據,還要插入到上一層的鏈表中,保證查詢效率。
redis 中使用了跳表來實現zset,redis中使用一個隨機算法來計算層級,計算出每個節點到底多少層索引,雖然不能絕對保證比較平衡,但是基本保證了效率,實現起來比那些平衡樹,紅黑樹的算法簡單一點。
棧
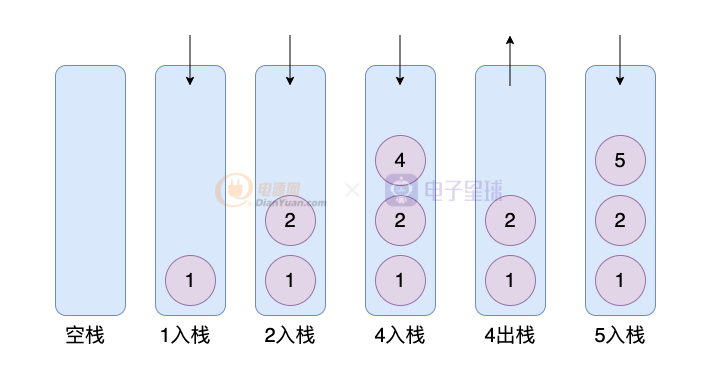
棧是一種數據結構,在Java里面體現是Stack類。它的本質是先進后出,就像是一個桶,只能不斷的放在上面,取出來的時候,也只能不斷的取出最上面的數據。要想取出底層的數據,只有等到上面的數據都取出來,才能做到。當然,如果有這種需求,我們一般會使用雙向隊列。
以下是棧的特性演示:
棧的底層用什么實現的?其實可以用鏈表,也可以用數組,但是JDK底層的棧,是用數組實現的,封裝之后,通過API操作的永遠都只能是最后一個元素,棧經常用來實現遞歸的功能。如果想要了解Java里面的棧或者其他集合實現分析,可以看看這系列文章:http://aphysia.cn/categories/collection
元素加入稱之為入棧(壓棧),取出元素,稱之為出棧,棧頂元素則是最后一次放進去的元素。
使用數組實現簡單的棧(注意僅供參考測試,實際會有線程安全等問題):
import java.util.Arrays;
public class MyStack<T> {
private T[] data;
private int length = 2;
private int maxIndex;
public MyStack() {
data = (T[]) new Object[length];
maxIndex = -1;
}
public void push(T element) {
if (isFull()) {
length = 2 * length;
data = Arrays.copyOf(data, length);
}
data[maxIndex + 1] = element;
maxIndex++;
}
public T pop() {
if (isEmpty()) {
throw new IndexOutOfBoundsException("棧內沒有數據");
} else {
T[] newdata = (T[]) new Object[data.length - 1];
for (int i = 0; i < data.length - 1; i++) {
newdata[i] = data[i];
}
T element = data[maxIndex];
maxIndex--;
data = newdata;
return element;
}
}
private boolean isFull() {
return data.length - 1 == maxIndex;
}
public boolean isEmpty() {
return maxIndex == -1;
}
public void display() {
for (int i = 0; i < data.length; i++) {
System.out.print(data[i]+" ");
}
System.out.println("");
}
}
測試代碼:
public class MyStackTest {
public static void main(String[] args) {
MyStack<Integer> myStack = new MyStack<>();
myStack.push(1);
myStack.push(2);
myStack.push(3);
myStack.push(4);
myStack.display();
System.out.println(myStack.pop());
myStack.display();
}
}
輸出結果如下,符合預期:
1 2 3 4
4
1 2 3
棧的特點就是先進先出,但是如果需要隨機取出前面的數據,效率會比較低,需要倒騰出來,但是如果底層使用數組,理論上是可以通過索引下標取出的,Java里面正是這樣實現。
隊列
既然前面有先進后出的數據結構,那我們必定也有先進先出的數據結構,疫情的時候,排隊估計大家都有測過核酸,那排隊老長了,排在前面先測,排在后面后測,這道理大家都懂。

隊列是一種特殊的線性表,特殊之處在于它只允許在表的前端(front)進行刪除操作,而在表的后端(rear)進行插入操作,和棧一樣,隊列是一種操作受限制的線性表。進行插入操作的端稱為隊尾,進行刪除操作的端稱為隊頭。
隊列的特點是先進先出,以下是例子:
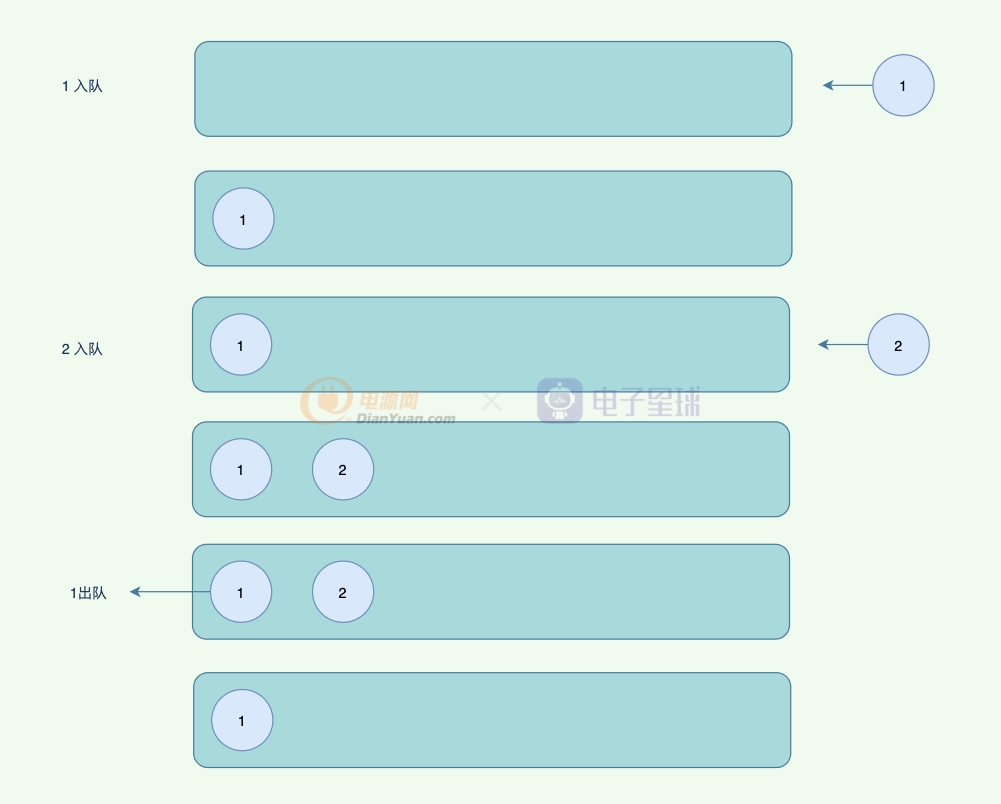
一般只要說到先進先出(FIFO),全稱First In First Out,就會想到隊列,但是如果你想擁有隊列即可以從隊頭取出元素,又可以從隊尾取出元素,那就需要用到特殊的隊列(雙向隊列),雙向隊列一般使用雙向鏈表實現會簡單一點。
下面我們用Java實現簡單的單向隊列:
class Node<T> {
public T data;
public Node next;
public Node(T data) {
this.data = data;
}
}
public class MyQueue<T> {
private Node<T> head;
private Node<T> rear;
private int size;
public MyQueue() {
size = 0;
}
public void pushBack(T element) {
Node newNode = new Node(element);
if (isEmpty()) {
head = newNode;
} else {
rear.next = newNode;
}
rear = newNode;
size++;
}
public boolean isEmpty() {
return head == null;
}
public T popFront() {
if (isEmpty()) {
throw new NullPointerException("隊列沒有數據");
} else {
Node<T> node = head;
head = head.next;
size--;
return node.data;
}
}
public void dispaly() {
Node temp = head;
while (temp != null) {
System.out.print(temp.data +" -> ");
temp = temp.next;
}
System.out.println("");
}
}
測試代碼如下:
public class MyStackTest {
public static void main(String[] args) {
MyStack<Integer> myStack = new MyStack<>();
myStack.push(1);
myStack.push(2);
myStack.push(3);
myStack.push(4);
myStack.display();
System.out.println(myStack.pop());
myStack.display();
}
}
運行結果:
1 -> 2 -> 3 ->
1
2 -> 3 ->
2
3 ->
常用的隊列類型如下:
- 單向隊列:也就是我們說的普通隊列,先進先出。
- 雙向隊列:可以從不同方向進出隊列
- 優先隊列:內部是自動排序的,按照一定順序出隊列
- 阻塞隊列:從隊列取出元素的時候,隊列沒有元素則會阻塞,同樣如果隊列滿了,往隊列里面放入元素也會被阻塞。
- 循環隊列:可以理解為一個循環鏈表,但是一般需要標識出頭尾節點,防止死循環,尾節點的next指向頭結點。
隊列一般可以用來保存需要順序的數據,或者保存任務,在樹的層次遍歷中可以使用隊列解決,一般廣度優先搜索都可以使用隊列解決。
哈希表
前面的數據結構,查找的時候,一般都是使用=或者!=,在折半查找或者其他范圍查詢的時候,可能會使用<和>,理想的時候,我們肯定希望不經過任何的比較,直接能定位到某個位置(存儲位置),這種在數組中,可以通過索引取得元素。那么,如果我們將需要存儲的數據和數組的索引對應起來,并且是一對一的關系,那不就可以很快定位到元素的位置了么?
只要通過函數f(k)就能找到k對應的位置,這個函數f(k)就是hash函數。它表示的是一種映射關系,但是對不同的值,可能會映射到同一個值(同一個hash地址),也就是f(k1) = f(k2),這種現象我們稱之為沖突或者碰撞。
hash表定義如下:
散列表(Hash table,也叫哈希表),是根據鍵(Key)而直接訪問在內存儲存位置的數據結構。也就是說,它通過計算一個關于鍵值的函數,將所需查詢的數據映射到表中一個位置來訪問記錄,這加快了查找速度。這個映射函數稱做散列函數,存放記錄的數組稱做散列表。
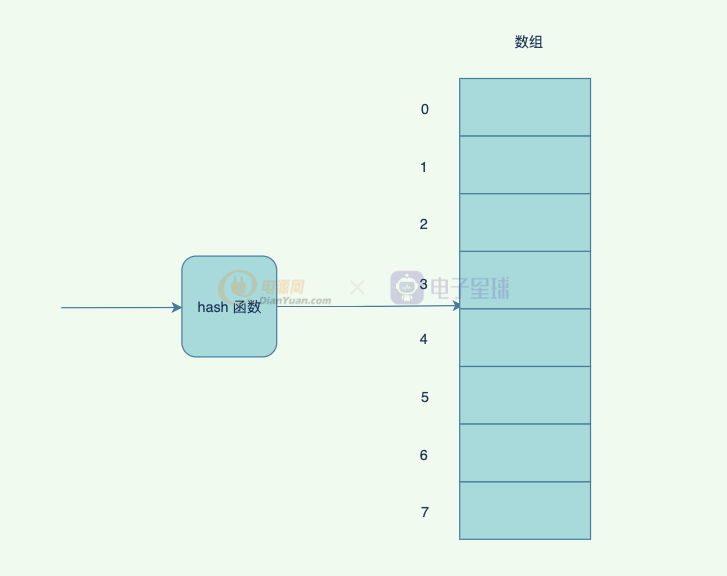
一般常用的hash 函數有:
- 直接定址法:取出關鍵字或者關鍵字的某個線性函數的值為哈希函數,比如H(key) = key或者H(key) = a * key + b
- 數字分析法:對于可能出現的數值全部了解,取關鍵字的若干數位組成哈希地址
- 平方取中法:取關鍵字平方后的中間幾位作為哈希地址
- 折疊法:將關鍵字分割成為位數相同的幾部分(最后一部分的位數可以不同),取這幾部分的疊加和(舍去進位),作為哈希地址。
- 除留余數法:取關鍵字被某個不大于散列表表長m的數p除后所得的余數為散列地址。即hash(k)=k mod p,p< =m。不僅可以對關鍵字直接取模,也可在折疊法、平方取中法等運算之后取模。對p的選擇很重要,一般取素數或m,若p選擇不好,容易產生沖突。
- 隨機數法:取關鍵字的隨機函數值作為它的哈希地址。
但是這些方法,都無法避免哈希沖突,只能有意識的減少。那處理hash沖突,一般有哪些方法呢?
- 開放地址法:hash計算后,如果該位置已經有數據,那么對該地址+1,也就是往后找,知道找到一個空的位置。
- 重新hash法:發生哈希沖突后,可以使用另外的hash函數重新極計算,找到空的hash地址,如果有,還可以再疊加hash函數。
- 鏈地址法:所有hash值一樣的,鏈接成為一個鏈表,掛在數組后面。
- 建立公共溢出區:不常見,意思是所有元素,如果和表中的元素hash沖突,都弄到另外一個表,也叫溢出表。
Java里面,用的就是鏈地址法:
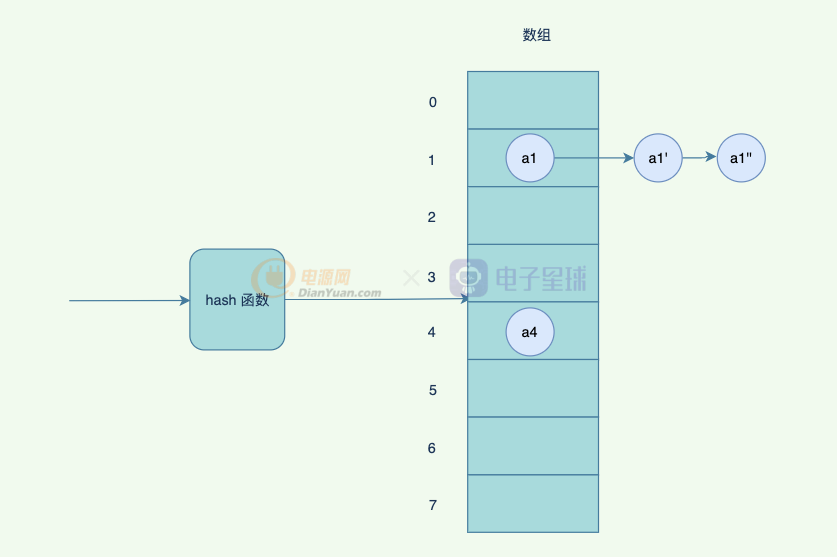
但是如果hash沖突比較嚴重,鏈表會比較長,查詢的時候,需要遍歷后面的鏈表,因此JDK優化了一版,鏈表的長度超過閾值的時候,會變成紅黑樹,紅黑樹有一定的規則去平衡子樹,避免退化成為鏈表,影響查詢效率。
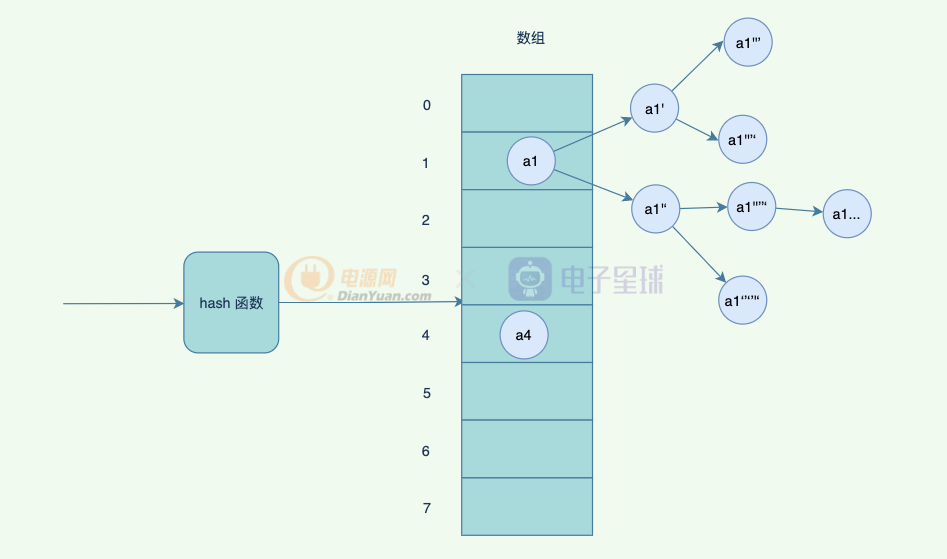
但是你肯定會想到,如果數組太小了,放了比較多數據了,怎么辦?再放沖突的概率會越來越高,其實這個時候會觸發一個擴容機制,將數組擴容成為 2倍大小,重新hash以前的數據,哈希到不同的數組中。
hash表的優點是查找速度快,但是如果不斷觸發重新 hash, 響應速度也會變慢。同時,如果希望范圍查詢,hash表不是好的選擇。
樹
數組和鏈表都是線性結構,而這里要介紹的樹,則是非線性結構。現實中樹是金字塔結構,數據結構中的樹,最上面稱之為根節點。

我們該如何定義樹結構呢?
樹是一種數據結構,它是由n(n≥1)個有限節點組成一個具有層次關系的集合。把它叫做“樹”是因為它看起來像一棵倒掛的樹,也就是說它是根朝上,而葉朝下的。它具有以下的特點:
每個節點有零個或多個子節點;沒有父節點的節點稱為根節點;每一個非根節點有且只有一個父節點;除了根節點外,每個子節點可以分為多個不相交的子樹。(百度百科)
下面是樹的基本術語(來自于清華大學數據結構C語言版):
- 節點的度:一個節點含有的子樹的個數稱為該節點的度
- 樹的度:一棵樹中,最大的節點度稱為樹的度;
- 葉節點或終端節點:度為零的節點;
- 非終端節點或分支節點:度不為零的節點;
- 父親節點或父節點:若一個節點含有子節點,則這個節點稱為其子節點的父節點;
- 孩子節點或子節點:一個節點含有的子樹的根節點稱為該節點的子節點;
- 兄弟節點:具有相同父節點的節點互稱為兄弟節點;
- 節點的層次:從根開始定義起,根為第1層,根的子節點為第2層,以此類推;
- 深度:對于任意節點n,n的深度為從根到n的唯一路徑長,根的深度為0;
- 高度:對于任意節點n,n的高度為從n到一片樹葉的最長路徑長,所有樹葉的高度為0;
- 堂兄弟節點:父節點在同一層的節點互為堂兄弟;
- 節點的祖先:從根到該節點所經分支上的所有節點;
- 子孫:以某節點為根的子樹中任一節點都稱為該節點的子孫。
- 有序樹:將樹種的節點的各個子樹看成從左至右是有次序的(不能互換),則應該稱該樹為有序樹,否則為無序樹
- 第一個孩子:在有序樹中最左邊的子樹的根稱為第一個孩子
- 最后一個孩子:在有序樹種最右邊的子樹的根稱為最后一個孩子
- 森林:由m(m>=0)棵互不相交的樹的集合稱為森林;
樹,其實我們最常用的是二叉樹:
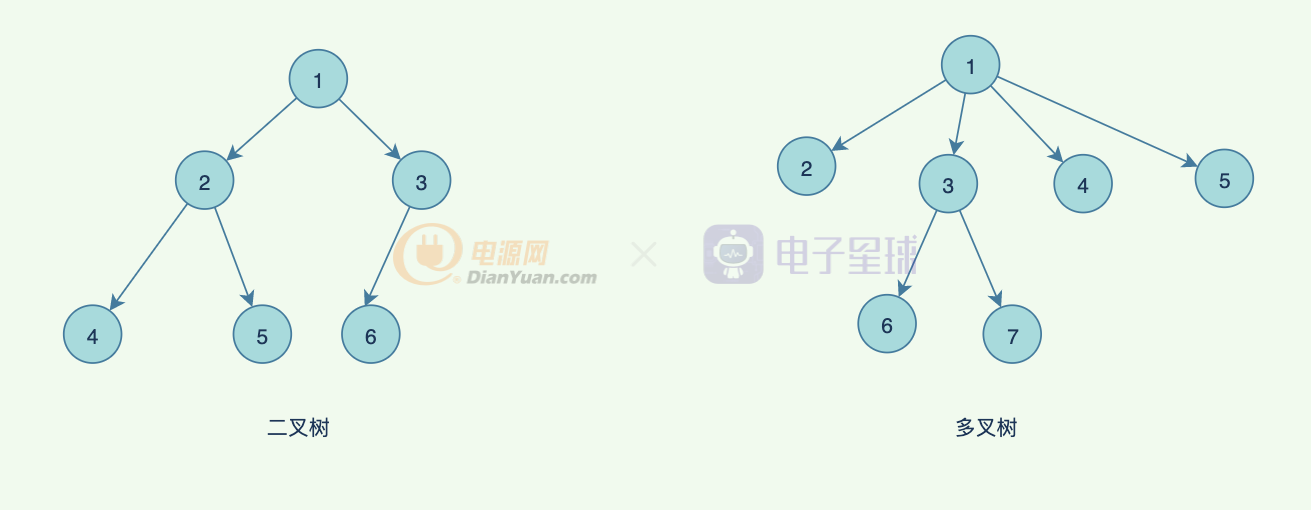
二叉樹的特點是每個節點最多只有兩個子樹,并且子樹有左右之分,左右子節點的次序不能任意顛倒。
二叉樹在Java中表示:
public class TreeLinkNode {
int val;
TreeLinkNode left = null;
TreeLinkNode right = null;
TreeLinkNode next = null;
TreeLinkNode(int val) {
this.val = val;
}
}
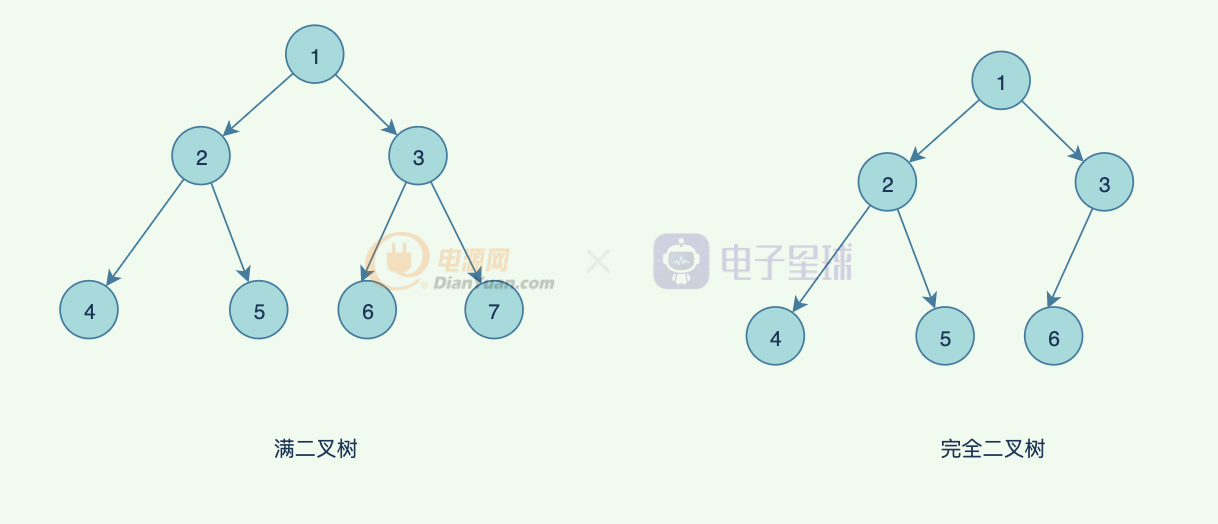
滿二叉樹:一棵深度為 k 且有 2k-1 個節點的二叉樹,稱之為滿二叉樹
完全二叉樹:深度為 k 的,有 n 個節點的二叉樹,當且僅當其每一個節點都與深度為 k 的滿二叉樹中編號從 1 到 n 的節點一一對應是,稱之為完全二叉樹。
一般二叉樹的遍歷有幾種:
- 前序遍歷:遍歷順序 根節點 --> 左子節點 --> 右子節點
- 中序遍歷:遍歷順序 左子節點 --> 根節點 --> 右子節點
- 后序遍歷:遍歷順序 左子節點 --> 右子節點 --> 根節點
- 廣度 / 層次遍歷: 從上往下,一層一層的遍歷
如果是一棵混亂的二叉樹,那查找或者搜索的效率也會比較低,和一條混亂的鏈表沒有什么區別,何必弄更加復雜的結構呢?
其實,二叉樹是可以用在排序或者搜索中的,因為二叉樹有嚴格的左右子樹之分,我們可以定義根節點,左子節點,右子節點的大小之分。于是有了二叉搜索樹:
二叉查找樹(Binary Search Tree),(又:二叉搜索樹,二叉排序樹)它或者是一棵空樹,或者是具有下列性質的二叉樹: 若它的左子樹不空,則左子樹上所有結點的值均小于它的根結點的值; 若它的右子樹不空,則右子樹上所有結點的值均大于它的根結點的值; 它的左、右子樹也分別為二叉排序樹。二叉搜索樹作為一種經典的數據結構,它既有鏈表的快速插入與刪除操作的特點,又有數組快速查找的優勢;所以應用十分廣泛,例如在文件系統和數據庫系統一般會采用這種數據結構進行高效率的排序與檢索操作。
二叉查找樹樣例如下:
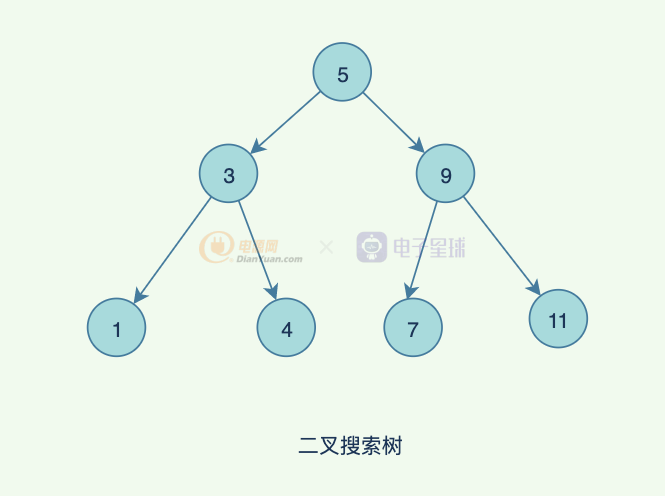
比如上面的樹,如果我們需要查找到 4, 從 5開始,4比5小,往左子樹走,查找到3,4比3大,往右子樹走,找到了4,也就是一個 7個節點的樹,我們只查找了3次,也就是層數,假設n個節點,那就是log(n+1)。
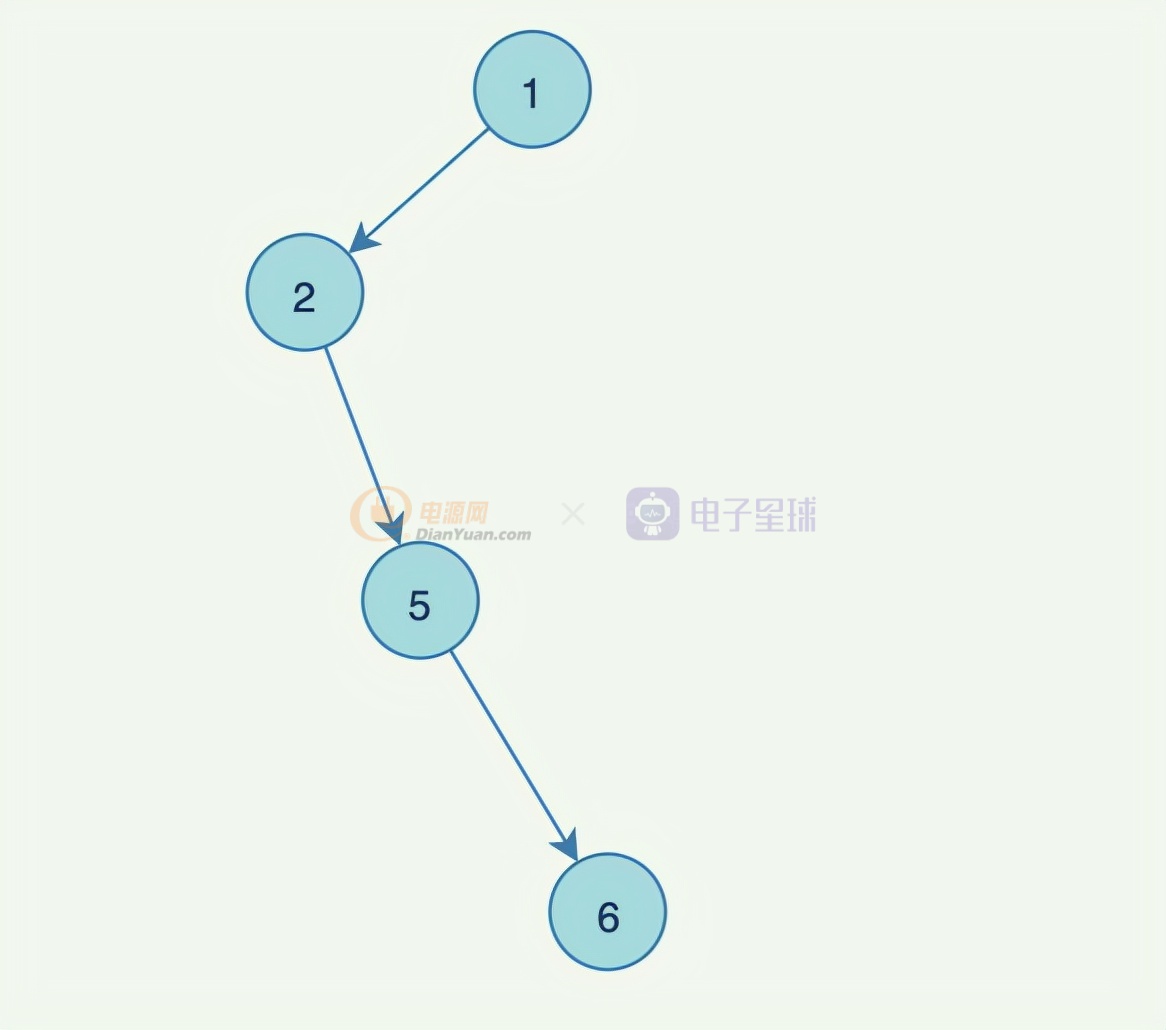
樹維護好了,查詢效率固然高,但是如果樹沒維護好,容易退化成為鏈表,查詢效率也會下降,比如:
一棵對查詢友好的二叉樹,應該是一個平衡或者接近平衡的二叉樹,何為平衡二叉樹:
平衡二叉搜索樹的任何結點的左子樹和右子樹高度最多相差1。平衡二叉樹也稱為 AVL 樹。
為了保證插入或者刪除數據等之后,二叉樹還是平衡二叉樹,那么就需要調整節點,這個也稱為平衡過程,里面會涉及各種旋轉調整,這里暫時不展開。
但是如果涉及大量的更新,刪除操作,平衡樹種的各種調整需要犧牲不小的性能,為了解決這個問題,有大佬提出了紅黑樹.
紅黑樹(Red Black Tree) 是一種自平衡二叉查找樹,是在計算機科學中用到的一種數據結構,典型的用途是實現關聯數組。 [1]
紅黑樹是在1972年由[Rudolf Bayer](https://baike.baidu.com/item/Rudolf Bayer/3014716)發明的,當時被稱為平衡二叉B樹(symmetric binary B-trees)。后來,在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改為如今的“紅黑樹”。 [2]
紅黑樹是一種特化的AVL樹(平衡二叉樹),都是在進行插入和刪除操作時通過特定操作保持二叉查找樹的平衡,從而獲得較高的查找性能。
紅黑樹有以下的特點:
- 性質1. 結點是紅色或黑色。
- 性質2. 根結點是黑色。
- 性質3. 所有葉子都是黑色。(葉子是NIL結點)
- 性質4. 每個紅色結點的兩個子結點都是黑色。(從每個葉子到根的所有路徑上不能有兩個連續的紅色結點)
- 性質5. 從任一節結點其每個葉子的所有路徑都包含相同數目的黑色結點。
正是這些特性,讓紅黑樹在調整的時候,不像普通的平衡二叉樹調整那般困難,頻繁。也就是加上了條條框框,讓它符合一定的標準,減少平衡過程的混亂以及頻次。
前面說的哈希表,Java 中的實現,正是應用了紅黑樹,在hash沖突較多的時候,會將鏈表轉換成為紅黑樹。
上面說的都是二叉樹,但是我們不得不扯一下多叉樹,為什么呢?雖然二叉樹中的各種搜索樹,紅黑樹已經很優秀了,但是在與磁盤交互的時候,大多數是數據存儲中,我們不得不考慮 IO 的因素,因為磁盤IO比內存慢太多了。如果索引樹的層高有幾千上萬,那么磁盤讀取的時候,需要次數太多了。B樹更加適合磁盤存儲。
970年,R.Bayer和E.mccreight提出了一種適用于外查找的樹,它是一種平衡的多叉樹,稱為B樹(或B-樹、B_樹)。
一棵m階B樹(balanced tree of order m)是一棵平衡的m路搜索樹。它或者是空樹,或者是滿足下列性質的樹:
1、根結點至少有兩個子女;
2、每個非根節點所包含的關鍵字個數 j 滿足:m/2 - 1 <= j <= m - 1;
3、除根結點以外的所有結點(不包括葉子結點)的度數正好是關鍵字總數加1,故內部子樹個數 k 滿足:m/2 <= k <= m ;
4、所有的葉子結點都位于同一層。
每個節點放多一點數據,查找的時候,內存中的操作比磁盤快很多,b樹可以減少磁盤IO的次數。B 樹:
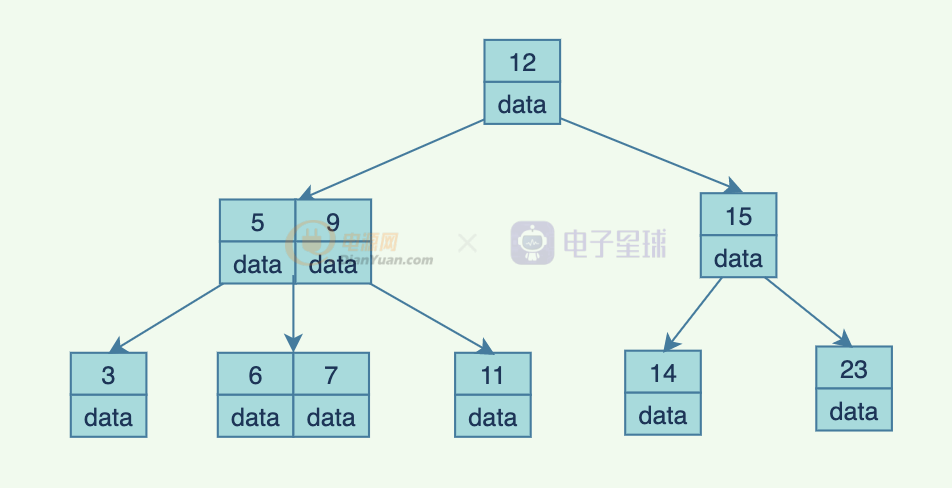
而每個節點的data可能很大,這樣會導致每一頁查出來的數據很少,IO查詢次數自然就增加了,那我們不如只在葉子節點中存儲數據:
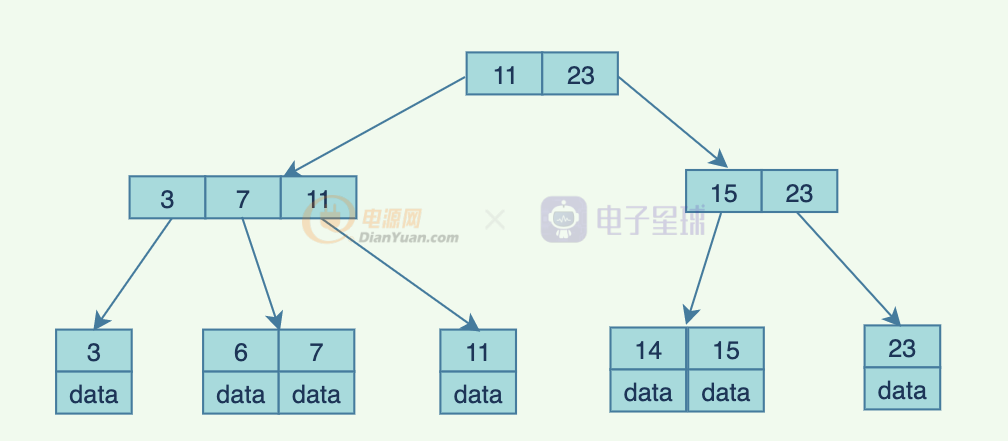
B+樹是B樹的一種變形形式,B+樹上的葉子結點存儲關鍵字以及相應記錄的地址,葉子結點以上各層作為索引使用。一棵m階的B+樹定義如下:
(1)每個結點至多有m個子女;
(2)除根結點外,每個結點至少有[m/2]個子女,根結點至少有兩個子女;
(3)有k個子女的結點必有k個關鍵字。
一般b+樹的葉子節點,會用鏈表連接起來,方便遍歷以及范圍遍歷。
這就是b+樹,b+樹相對于B樹多了以下優勢:
- b+樹的中間節點不保存數據,每次IO查詢能查到更多的索引,,是一個矮胖的樹。
- 對于范圍查找來說,b+樹只需遍歷葉子節點鏈表即可,b樹卻需要從根節點都葉子節點。
除了上面的樹,其實還有一種叫Huffman樹:給定N個權值作為N個葉子結點,構造一棵二叉樹,若該樹的帶權路徑長度達到最小,稱這樣的二叉樹為最優二叉樹,也稱為哈夫曼樹(Huffman Tree)。哈夫曼樹是帶權路徑長度最短的樹,權值較大的結點離根較近。
一般用來作為壓縮使用,因為數據中,每個字符出現的頻率不一樣,出現頻率越高的字符,我們用越短的編碼保存,就可以達到壓縮的目的。那這個編碼怎么來的呢?
假設字符是hello,那么編碼可能是(只是編碼的大致雛形,高頻率出現的字符,編碼更短),編碼就是從根節點到當前字符的路徑的01串:
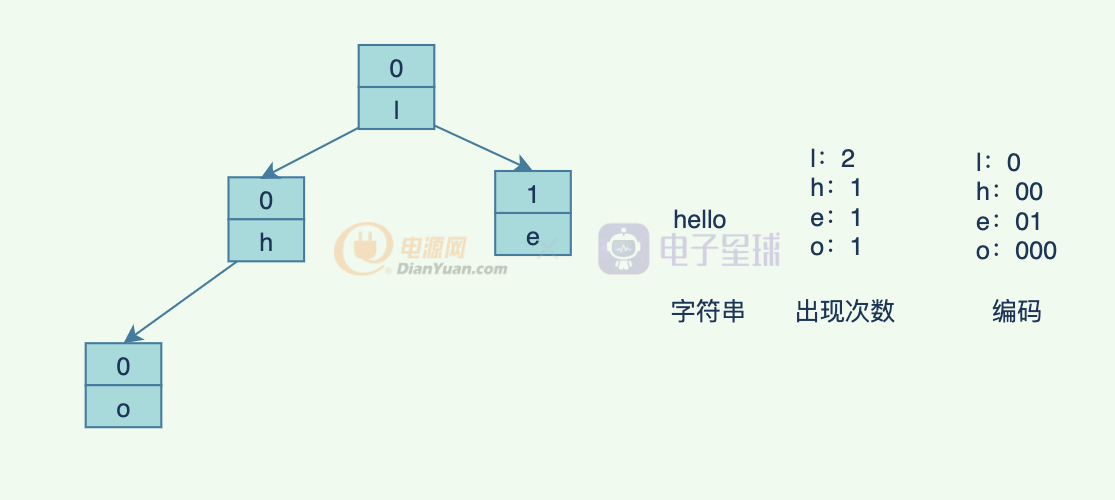
通過不同權值的編碼,哈夫曼樹到了有效的壓縮。
堆
堆,其實也是二叉樹中的一種,堆必須是完全二叉樹,完全二叉樹是:除了最后一層,其他層的節點個數都是滿的,最后一層的節點都集中在左部連續位置。
而堆還有一個要求:堆中每一個節點的值都必須大于等于(或小于等于)其左右子節點的值。
堆主要分為兩種:
- 大頂堆:每個節點都大于等于其子樹節點(堆頂是最大值)
- 小頂堆:每個節點都小于等于其子樹節點(堆頂是最小值)
一般情況下,我們都是用數組來表示堆,比如下面的小頂堆:
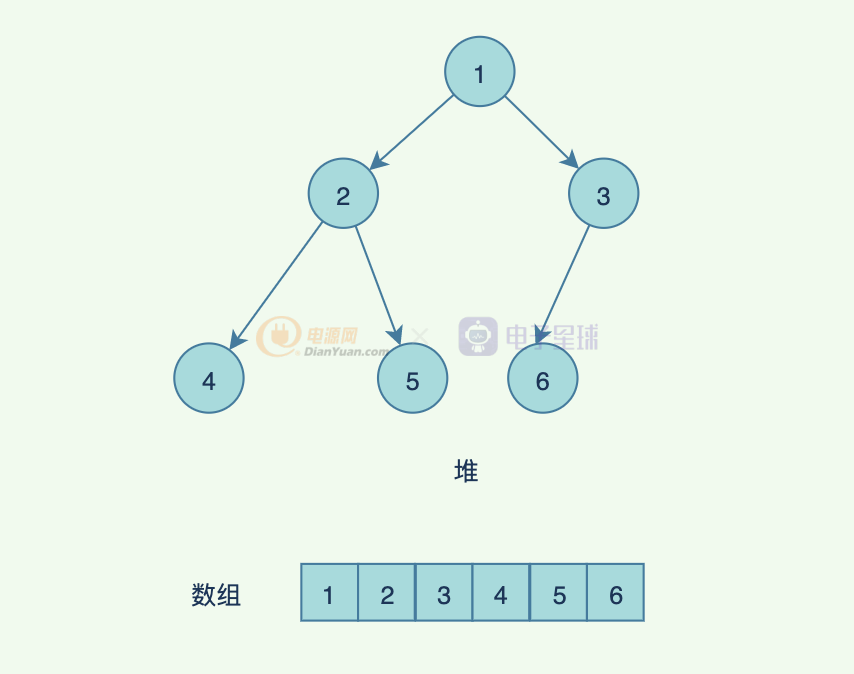
數組中父子節點以及左右節點的關系如下:
- i 結點的父結點 parent = floor((i-1)/2) (向下取整)
- i 結點的左子結點 2 * i +1
- i 結點的右子結點 2 * i + 2
既然是存儲數據的,那么一定會涉及到插入刪除等操作,堆里面插入刪除,會涉及到堆的調整,調整之后才能重新滿足它的定義,這個調整的過程,叫做堆化。
用小頂堆舉例,調整主要是為了保證:
- 還是完全二叉樹
- 堆中每一個節點都還小于等于其左右子節點
對于小頂堆,調整的時候是:小元素往上浮,大元素往下沉,就是不斷交換的過程。
堆一般可以用來求解TOP K 問題,或者前面我們說的優先隊列等。
圖
終于來到了圖的講解,圖其實就是二維平面,之前寫過掃雷,掃雷的整個方塊區域,其實也可以說是圖相關的。圖是非線性的數據結構,主要是由邊和頂點組成。
同時圖又分為有向圖與無向圖,上面的是無向圖,因為邊沒有指明方向,只是表示兩者關聯關系,而有向圖則是這樣:
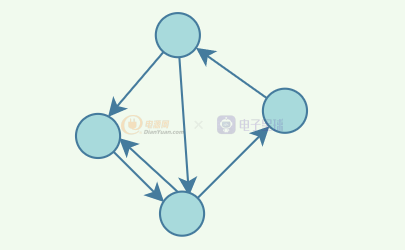
如果每個頂點是一個地方,每條邊是路徑,那么這就是一張地圖網絡,因此圖也經常被用于求解最短距離。先來看看圖相關的概念:
- 頂點:圖最基本的單元,那些節點
- 邊:頂點之間的關聯關系
- 相鄰頂點:由邊直接關聯的頂點
- 度:一個頂點直接連接的相鄰頂點的數量
- 權重:邊的權值
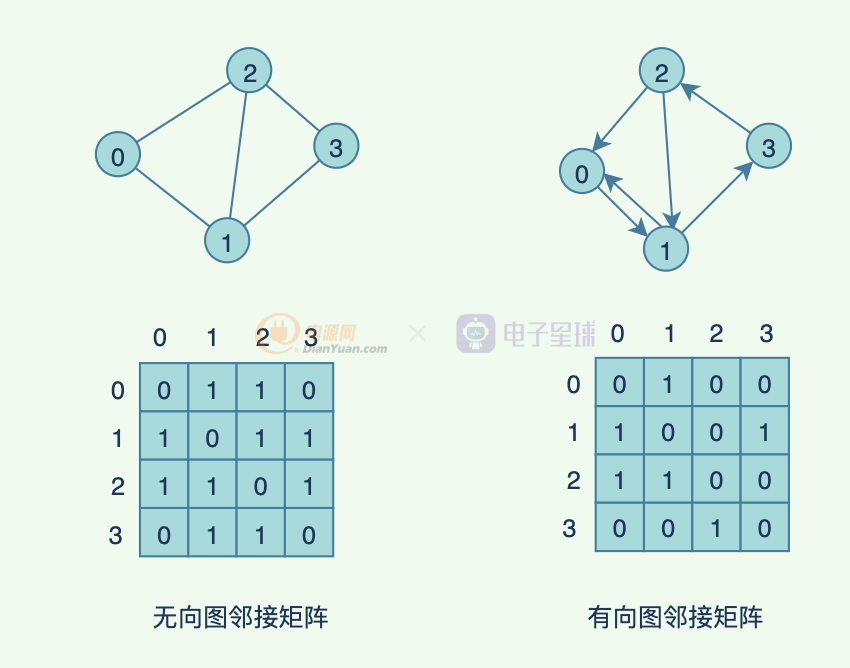
一般表示圖有以下幾種方法:
- 鄰接矩陣,使用二維數組表示,為1 表示聯通,0表示不連通,當然如果表示路徑長度的時候,可以用大于0的數表示路徑長度,用-1表示不連通。
下面的圖片中,0和 1,2連通,我們可以看到第 0行的第1,2列是1 ,表示連通。還有一點:頂點自身我們是標識了0,表示不連通,但是有些情況可以視為連通狀態。
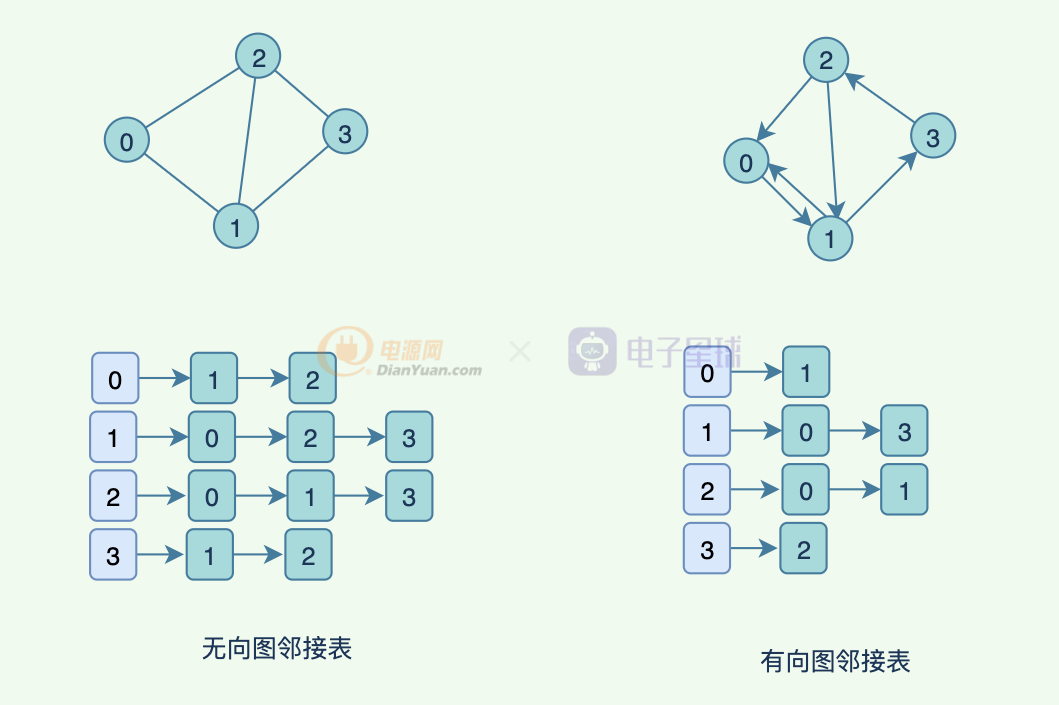
- 鄰接表
鄰接表,存儲方法跟樹的孩子鏈表示法相類似,是一種順序分配和鏈式分配相結合的存儲結構。如這個表頭結點所對應的頂點存在相鄰頂點,則把相鄰頂點依次存放于表頭結點所指向的單向鏈表中。
對于無向圖來說,使用鄰接表進行存儲也會出現數據冗余,表頭結點A所指鏈表中存在一個指向C的表結點的同時,表頭結點C所指鏈表也會存在一個指向A的表結點。
圖里面遍歷一般分為廣度優先遍歷和深度優先遍歷,廣度優先遍歷是指優先遍歷與當前頂點直接相關的頂點,一般借助隊列實現。而深度優先遍歷則是往一個方向一直走到不能再走,有點不撞南墻不回頭的意思,一般使用遞歸實現。
圖,除了用了計算最小路徑以外,還有一個概念:最小生成樹。
一個有 n 個結點的連通圖的生成樹是原圖的極小連通子圖,且包含原圖中的所有 n 個結點,并且有保持圖連通的最少的邊。 最小生成樹可以用kruskal(克魯斯卡爾)算法或prim(普里姆)算法求出。
有一種說法,圖是平面上的點,我們把其中一個點拎起來,能將其他頂點帶起來的邊,取最小權值,多余的邊去掉,就是最小生成樹。
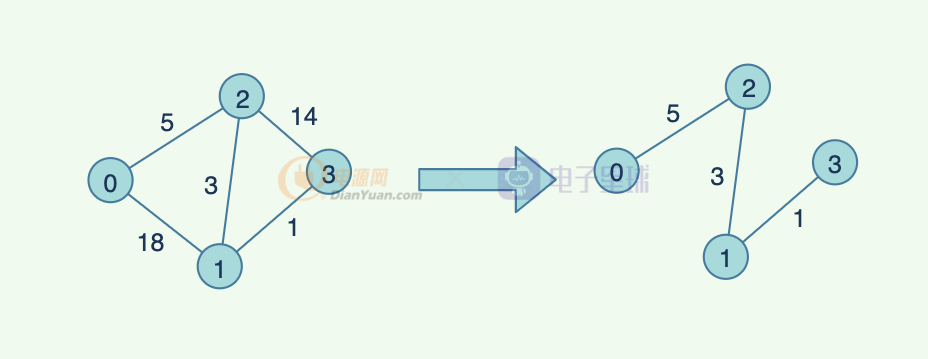
當然,最小生成樹并不一定是唯一的,可能存在多種結果。


