漏感是由變壓器中一個繞組的磁通量引起的，該磁通量不耦合到其他繞組。 這是由于繞組之間的空間和間隙中的磁通量將能量存儲在這些間隙中，就像能量存儲在鐵氧體磁芯的氣隙中一樣。 漏感中的能量通常耗散到變壓器外部。

對于反激變壓器，最小化漏電感非常重要，因為在大多數情況下漏電感 能量在外部緩沖器或鉗位電路中耗散。 正如您稍后將看到的，將漏電與磁化電感的比率降至最低以最大限度地減少鉗位電路損失的磁化能量也很重要。

一、如何估計和最小化漏電感

幾種已發表的方法解釋了如何根據繞組的物理幾何形狀和變壓器中的層結構來估計漏電感。 圖 1和公式顯示了使用夾層的方法。 此方法假設所有繞組層的全寬 b 相同，并且不能與某些部分寬度的層一起使用。 請注意，任何部分寬度層的漏電感都會高得多，隨著部分層寬度變窄而增加。

以下是公式的參數：

• N = 與泄漏有關的繞組匝數

• MLT = 每匝繞組的平均長度

• Σh = 所有繞組層的高度總和

• Σc = 繞組層間距的高度總和

• m = 交錯級別（繞組“部分”的數量）

• b = 骨架繞線寬度（繞線層的寬度）

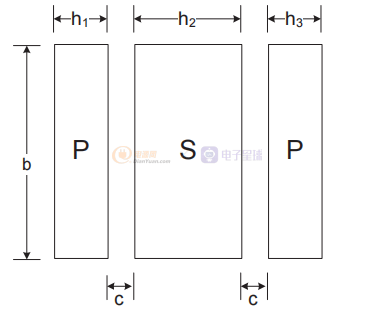
圖1 典型的交錯式反激變壓器繞組層間距

根據 Dowell 方程中使用的假設，圓形線徑 d 的每個繞組層都轉換為相同橫截面的等效矩形塊。 因此，h 與 d 并不完全相同：

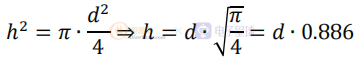
如圖 2所示，您可以使用線徑和公式來計算每個繞組層的 h。 您可以使用中間膠帶或絕緣體的厚度，加上電線上的厚度或漆包覆層或任何其他絕緣體，再加上由于直徑 d 轉換為等效的 h 而產生的額外間隙，從而計算間距 c。

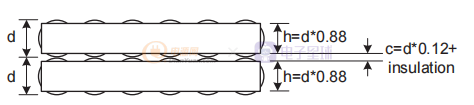
圖2 將每個繞組層對轉換為等效的 h 和 c 

二、漏電感減少和最小化

漏感很大程度上取決于物理繞組幾何形狀； 您可以根據此幾何形狀估算漏電感。 可以通過以下方式降低漏電感：

• 交錯——增加m 的值。 

• 使用更寬的繞線寬度——最大化b。 

• 最小化圈數 N 和每圈平均長度 MLT。

• 最小化繞組層之間的間距cn 的厚度和數量。

• 最小化繞組層厚度、hn 和層數。

三、交錯

圖3顯示了在傳統前向模式環境中降低漏電感的不同級別交錯的示例變壓器。 但同樣的原理也適用于轉換間隔期間的反激式變壓器，此時初級和次級電流同時流動，以及漏感相關時。

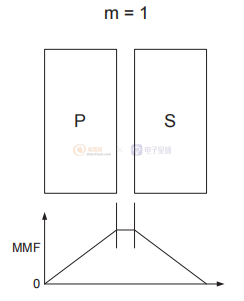
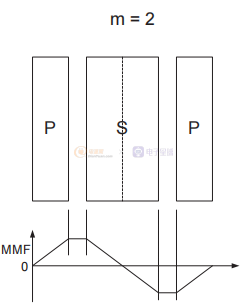
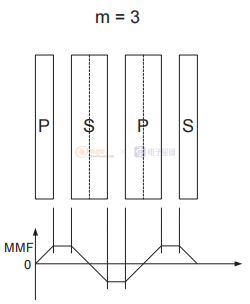
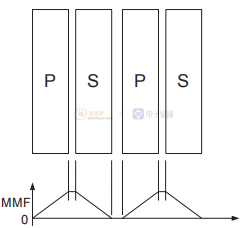
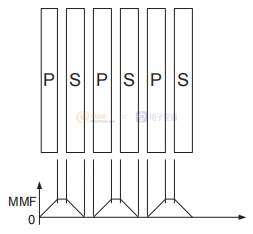
圖3 不同級別的交錯以減少漏感。

在第一個示例中，初級和次級并排放置，沒有交錯。 下面相應的 MMF 圖顯示了主要 MMF 如何建立到最大值，然后被次要 MMF 取消，回到零。 MMF 圖僅顯示 MMF 的一部分或區域累積并返回零 - 因此在此示例中，只有一部分，m = 1。

主要和次要在第二個示例中交錯。 兩種交織方法不同，但等效。 這是因為在這兩種情況下，MMF 在兩個不同的部分建立一個峰值并下降回零，所以在這兩種情況下 m = 2。類似地，第三個例子顯示了兩種不同的交織方法，但兩者在 交錯部分，兩種情況下 m = 3。

由于漏電感與 m2 成反比，因此預計第一級交錯兩部分（即 m = 2）會導致漏電感降低四倍。 通過從 m = 1 更改為 m = 2，如圖3所示，繞組結構從單個初級 - 次級界面變為兩個界面，次級的每個面都有一個界面。 在交錯情況下，現在有兩個界面間距間隙，c； 在非交錯情況下，兩者的維度可能與單個 c 的維度大致相同。 所以實際上，公式中的因子 Σc/m2 只減少了兩倍，而漏電感實際上只減少了一半。 盡管如此，這是一個顯著的減少，通常是非常有益的。

然而，設計人員應該意識到，初級和次級繞組交錯可能會增加變壓器成本，使 EMI 和安全合規性變得復雜（因為現在有兩個初級 - 次級接口），并增加變壓器繞組間電容。

四、漏電感估計 - 工作示例

我們現在使用公式來估計圖4中所示的典型反激式變壓器繞組結構的漏電感。該結構由分離的初級和夾在中間的輔助偏置層和次級層組成。 每個半初級纏繞在兩層上，次級和偏置層纏繞在單層上。 在次級和外半初級之間還有一個屏蔽層。 圖 4列出了所有電線尺寸。

圖4交錯式反激變壓器繞組結構。

我們將所有圓形線徑轉換為具有相同橫截面的等效矩形塊。 目標設計的開關頻率為 60 kHz，δ ~0.31 mm。 屏蔽層足夠薄（0.05 毫米，δ 的六分之一），因此為簡單起見，我們將其作為次級和外半初級之間的絕緣空間的一部分（圖 5）。

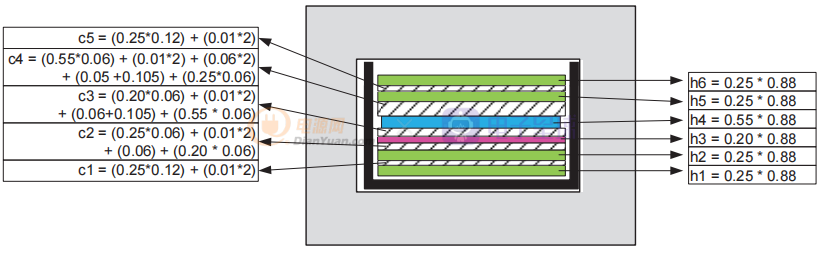
圖5 樣品交錯反激式變壓器繞組結構到層高hn和間距cn的轉換。

當您知道所有導電層的高度 hn 和絕緣層的間距 cn 時，您可以使用公式估算漏電感。在這種情況下，初級總匝數 N = 34； 我們使用了 RM10 線軸，MLT = 52 毫米。 原版由兩部分交錯，m = 2； 繞組寬度 b = 9 mm。 （線軸標稱尺寸實際上是 10 毫米，但由于導線絕緣和入口/出口導線布線，層填充通常是可用寬度的 90%）。

在公式中，2.71 µH 與測得的 3.2 µH 漏電感相當接近。 差異歸結為實際繞組的實際非理想性，例如膠帶壓痕、入口/出口厚度和返回線。 盡管如此，我們已經展示了如何估計給定繞組結構的漏電感，以及如何客觀地比較不同繞組結構的漏電感性能。 我們還展示了所選骨架形狀/幾何形狀對漏電感的影響。

五、鉗位電壓值對變壓器漏感損耗的影響

在單開關反激式轉換器中，您通常需要一個鉗位電路來限制開關的漏極電壓； 鉗位電路吸收存儲在變壓器漏電感中的能量，并且根據鉗位電壓的值，還會吸收一小部分磁化能量。在圖 6 中，您可以看到晶體管 Q 關斷后，所有的 初級電流轉移到鉗位電路（在圖6中由電壓源 VCLAMP 表示）。 漏電感 LLEAK 上將產生電壓，該電壓等于 VCLAMP 和反射次級電壓 VREFLECTED 之間的差值。 因此，漏電感中的電流（也是初級電流）將以取決于兩個電壓差的速率下降； 因此，磁化電流將流入鉗位電路，直到初級電流衰減為零。

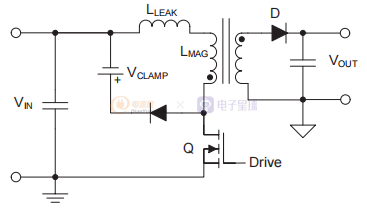
圖6 簡化的反激原理圖，顯示了作為理想電壓鉗位的鉗位/緩沖器網絡

漏電感中電流減小的速率決定了電流轉移到次級的速率。 圖7說明了這個過程。

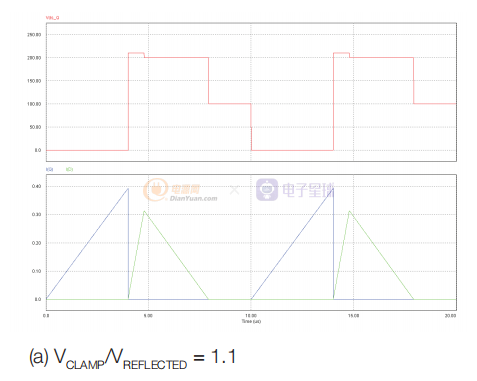
圖7 到次級繞組的電流傳輸 (a) 與電壓鉗位 (b) 的比較

在圖 7a 中，鉗位電壓僅比反射的次級電壓高 10%，在鉗位中損失了大量的磁化能量。 與圖 7b 相比，傳輸到次級的電流明顯較低，其中鉗位電壓比反射的次級電壓高 50%。

在極端情況下，反射的次級電壓等于鉗位電壓，沒有電壓可用于 迫使漏電感中的電流比磁化電感中的電流衰減得更快； 因此，沒有磁化電流可以傳輸到次級。 鉗位電路將吸收所有磁化能量和泄漏能量。

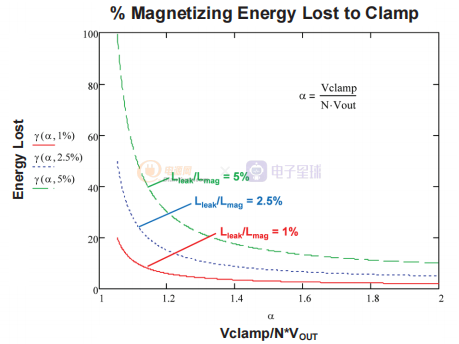
圖8 鉗位能量損失百分比與鉗位電平和漏感/磁化電感比的圖表。

圖 8顯示了鉗位中磁化能量損失的百分比 γ，它是鉗位電壓與初級反射電壓之比 α 以及漏電流與磁化電感的百分比的函數。

鉗位中的能量損失 隨著鉗位與反射電壓的比率下降到 1.2 以下，它迅速增加。 這種損耗對漏磁電感比也非常敏感。

雖然選擇較低的鉗位電壓可能允許使用具有較低 RDS(on) 的低壓開關晶體管，但增加的鉗位損耗很容易超過預期的好處。