多輸出反激式轉(zhuǎn)換器因其簡(jiǎn)單和低成本而成為一種流行的拓?fù)浣Y(jié)構(gòu)。 如果繞組之間的完美耦合是可能的，那么輸出電壓將直接由它們各自與提供穩(wěn)壓輸出的繞組的匝數(shù)比來定義。 不幸的是，完美的繞組耦合是不可能的，耦合操作非常復(fù)雜，這往往會(huì)導(dǎo)致交叉調(diào)節(jié)不佳。本文就來揭開交叉調(diào)整率的神秘面紗！

一、理論分析

有一些已知的交叉調(diào)節(jié)分析模型。例如，使用物理模型的交叉調(diào)節(jié)分析相當(dāng)復(fù)雜，但具有幾何獨(dú)立性和其參數(shù)可以直接測(cè)量等優(yōu)點(diǎn)。另一方面，圖1中所示的物理模型（也稱為“梯形”模型）基于這樣一個(gè)事實(shí)，即變壓器繞組由于它們之間的物理分離而無(wú)法全部都很好地耦合到儲(chǔ)能間隙。此外，額外量的磁能存儲(chǔ)在繞組之間并表示為漏電感。盡管不適用于任何變壓器幾何結(jié)構(gòu)，但該模型是幫助了解大多數(shù)常見反激變壓器幾何結(jié)構(gòu)如何工作的好工具。圖 1中的電路表示僅適用于所示的變壓器繞組疊層。如果使用交錯(cuò)或同時(shí)纏繞多個(gè)次級(jí)繞組（多股），則需要更復(fù)雜的電路表示。此外，該模型在評(píng)估輕載次級(jí)輸出時(shí)確實(shí)缺乏準(zhǔn)確性。

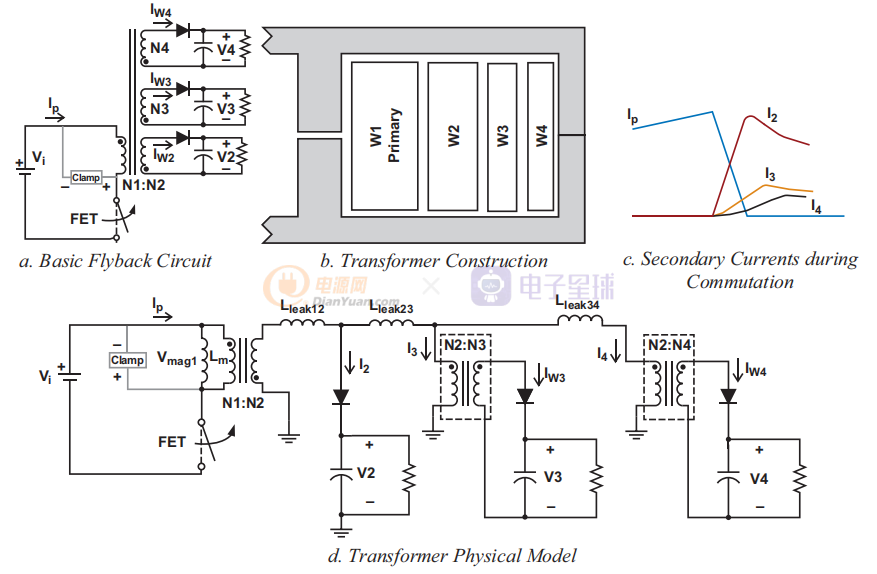
圖1 具有理想化次級(jí)電流波形的基于物理模型的反激交叉調(diào)節(jié)（所有輸出均處于滿載狀態(tài)；不包括繞組電阻和寄生電容效應(yīng)）。

在換向過程中，間隙中的磁通量 (φm) 會(huì)降低，從而在次級(jí)繞組中感應(yīng)出電流。 這種感應(yīng)電流有助于保持間隙中的磁動(dòng)勢(shì) (MMF)。 每個(gè)次級(jí)繞組內(nèi)的磁通下降率（包括漏感）受其輸出電壓的限制，公式如下：

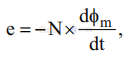
其中 N 是繞組的匝數(shù)，e 是其感應(yīng)電壓。

例如，一旦初級(jí)電壓超過 W2 的反射電壓，W2 的電流就會(huì)增加，進(jìn)而產(chǎn)生增加的通量。 由于 W1 和 W2 之間的漏磁通，初級(jí)電壓上升，直到達(dá)到鉗位電壓。 這定義了間隙中 dfm/dt 的限制。

主次級(jí)繞組 (W2) 與初級(jí) (W1) 相鄰，決定了外部繞組在換向過程中將看到的 df/dt。 由于 W3 和 W4 位于主輸出繞組之后，如果完全沒有泄漏，則產(chǎn)生的繞組電壓低于預(yù)期的電壓。 圖 1中顯示的凈效應(yīng)是，當(dāng)主開關(guān)關(guān)閉時(shí)，電流從近端到遠(yuǎn)端的次級(jí)繞組逐漸換向。

然而，如果采用交錯(cuò)方式，使 W1 的一半靠近低功率次級(jí)繞組，W1 的部分磁通將不會(huì)被 W2 檢測(cè)到，但會(huì)被低功率次級(jí)繞組檢測(cè)到，從而增加了 感應(yīng)到這些繞組中的電壓。

在所示模型中，當(dāng)所有泄漏都移到變壓器的 W2 側(cè)時(shí)，Lleak12 對(duì)應(yīng)于 W2 和 W1 之間的漏電感，而 Lleak23 和 Lleak34 分別對(duì)應(yīng)于 W2 到 W3 和 W3 到 W4 之間的泄漏。

二、漏感和寄生電容引起的振鈴

大多數(shù)現(xiàn)有模型無(wú)法準(zhǔn)確預(yù)測(cè)反激變壓器的一種行為——主輸出滿載時(shí)輔助繞組的輕載運(yùn)行。

當(dāng)主開關(guān)關(guān)閉時(shí)，當(dāng)主輸出負(fù)載很重時(shí)，初級(jí)電流會(huì)導(dǎo)致電壓迅速上升。 由于變壓器漏感和寄生電容（繞組和二極管），次級(jí)電壓趨于振鈴。 如果輔助輸出滿載，則此振鈴被鉗位。 然而，在輕負(fù)載時(shí)，這種振鈴開始通過輸出整流器將輸出存儲(chǔ)電容器充電至振鈴電壓過沖，從而阻止能量返回。 在輕載時(shí)，這會(huì)導(dǎo)致輔助輸出電壓高得多，有時(shí)甚至?xí)^其標(biāo)稱值的兩倍。 隨著初級(jí)鉗位電壓升高，這種影響通常會(huì)變得更糟。

對(duì)于反激電源來說，輕負(fù)載交叉調(diào)節(jié)問題可以通過最小化次級(jí)繞組之間的漏電感來減輕，但不能消除。 它還有助于找到最靠近初級(jí)的最高功率次級(jí)。 處理此問題的其他解決方案包括使用后置穩(wěn)壓器、串聯(lián)電阻或最小負(fù)載。 

三、工作影響

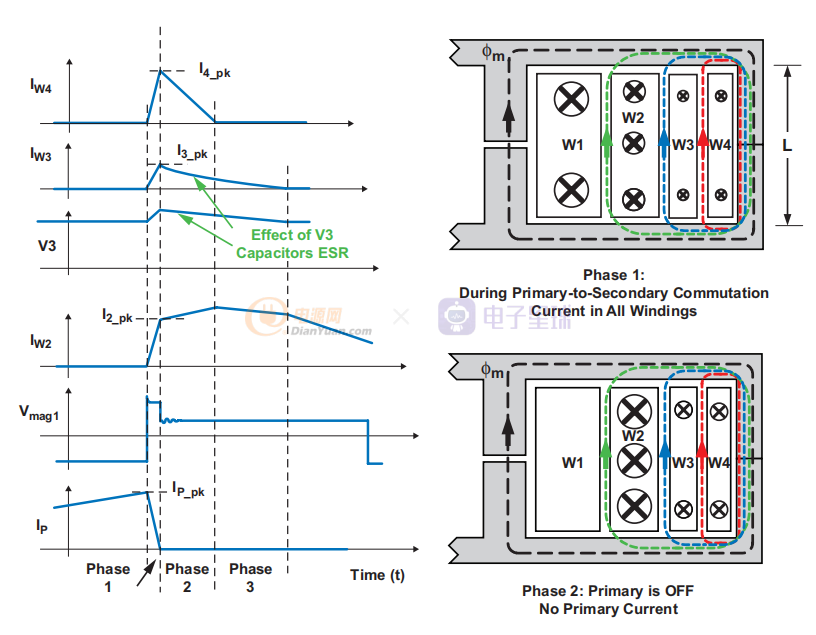
圖2初級(jí)開關(guān)關(guān)斷時(shí)的交叉調(diào)節(jié)階段

與圖 1 相對(duì)應(yīng)，圖 2 顯示了從初級(jí)到次級(jí)換向期間前三相的示例。 出于描述的目的，假設(shè)W2是大電流繞組，I2_pk不夠高，因?yàn)長(zhǎng)leak21太大，W4在換向過程中因?yàn)檩p載振鈴接收太多能量。 W3 和 W4 是低電流輔助次級(jí)繞組。

與正激變壓器不同，在反激變壓器中，初級(jí)和次級(jí)繞組僅在換向期間同時(shí)產(chǎn)生磁通； 該通量是磁化通量。 另一個(gè)區(qū)別是，在換向期間，間隙內(nèi)每個(gè)繞組產(chǎn)生的磁通方向相同，因?yàn)樵诔跫?jí)繞組電流逐漸下降時(shí)，所有繞組都試圖保持磁化通量。 因此，在繞組之間的間距（泄漏）中產(chǎn)生的磁通線彼此相對(duì)。 請(qǐng)注意，沿特定路徑的漏磁通幅度與 S(N × I) 和兩層之間的間距成正比，與圖2 所示窗口區(qū)域的尺寸 L 成反比。

如前所述，在換向過程中，磁通量 (φm) 的減少會(huì)在次級(jí)繞組中感應(yīng)出上升的電流。 由于 W1 和 W2 之間的泄漏，初級(jí)電壓上升直到達(dá)到鉗位電壓，這定義了間隙中 dfm/dt 的限制。 鉗位電壓越低，次級(jí)繞組中的感應(yīng)電壓越低，其中的 di/dt 越軟。 如果沒有初級(jí)鉗位電路，轉(zhuǎn)換到 W2 次級(jí)將是瞬時(shí)的，但 MOSFET 會(huì)被電壓應(yīng)力破壞。

在階段 1 結(jié)束時(shí)，反射的次級(jí)電流之和等于總磁化電流：

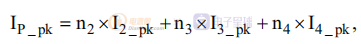
其中 Ix_pk 和 nx 分別是換向間隔結(jié)束時(shí)的電流和次級(jí)繞組數(shù) x 的初級(jí)與次級(jí)匝數(shù)比。

從第 2 階段和開關(guān)周期的剩余時(shí)間 (1 – D) 開始，次級(jí)電流以取決于反射輸出電壓之間差異的速率增加或減少。 在此示例中，假設(shè) I4_pk 變得太高，并且 V4 的輸出電容器在階段 1 期間接收了過多能量。在階段 2 開始時(shí)，一部分磁通來自 W4，并開始以 W4 電壓定義的速率下降 . 此外，W2 的貢獻(xiàn)增加以保持間隙中的磁化通量。 在此期間，IW4 下降，直到它過零并因二極管而停止下降。 如果一個(gè)輸出負(fù)載很輕，它的電壓會(huì)在換向過程中顯著增加。 這意味著在第 1 階段之后電流下降更陡峭（更快）。

每個(gè)輸出端的負(fù)載會(huì)極大地影響交叉調(diào)節(jié)。 輸出電容器 ESR 也具有不可忽略的影響，因?yàn)樗鼤?huì)隨著電流減小而改變斜率。 電流越小，ESR 電壓和漏電感兩端的電壓將越低，這意味著 di/dt 越低。 圖 2中 V3 和 IW3 的波形展示了這一概念。

當(dāng) IW4 過零時(shí) IW2 的斜率變化可以用以下公式解釋：

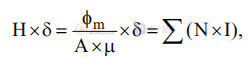
其中 H 是磁場(chǎng)，δ 是磁芯間隙，φm 是磁化通量，A 是磁芯橫截面，μ 是磁隙磁導(dǎo)率，N × I 是繞組的安匝數(shù)。 公式顯示下降的磁化通量 (fm) 對(duì)應(yīng)于所有有源繞組共享的下降的磁化電流。

顯然，在 CCM 中操作主輸出（使用同步整流器是一個(gè)例子）保證了 Vmag1 在 (1 – D) 期間保持不變，有助于實(shí)現(xiàn)更好的交叉調(diào)節(jié)。

后續(xù)文章我們討論如何優(yōu)化交叉調(diào)整率的具體措施。