2.2 BUCK DCM模式穩態分析
我們現在研究當負載電流降低時會發生什么。 首先,觀察功率級輸出電流是電感電流的平均值。這應該是顯而易見的,因為電感電流流入輸出電容和負載電阻組合,并且流入輸出電容的平均電流始終為零。
如果輸出負載電流降低到臨界電流水平以下,則電感電流在開關周期的一部分內將為零。從圖 3 所示的波形中可以明顯看出這一點,因為紋波電流的峰峰值幅度不隨輸出負載電流而變化。在(非同步)降壓功率級中,如果電感電流試圖降到零以下,它只會停在零(由于 CR1 中的單向電流)并保持在零,直到下一個開關周期開始。這種工作模式稱為不連續導通模式。在不連續導通模式下工作的功率級在每個開關周期具有三個獨特的狀態,而不是連續導通模式的兩個狀態。功率級處于連續模式和非連續模式之間的邊界時的負載電流條件如圖 4 所示。此時電感器電流降至零,并且在電流達到零后立即開始下一個開關周期。
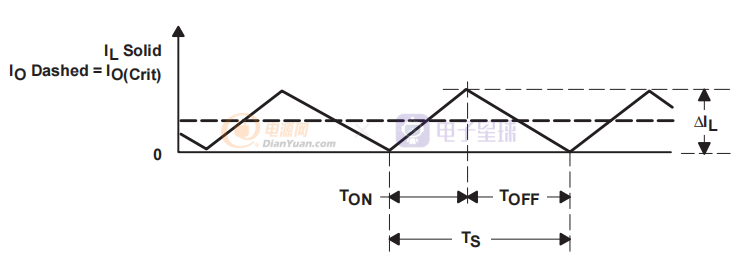
圖4 臨界模式BCM
輸出負載電流的進一步降低使功率級進入不連續導通模式。 這種情況如圖 5 所示。非連續模式功率級頻率響應與連續模式頻率響應完全不同,并在降壓功率級建模部分中顯示。 此外,輸入到輸出的關系也大不相同,如下面的推導所示。
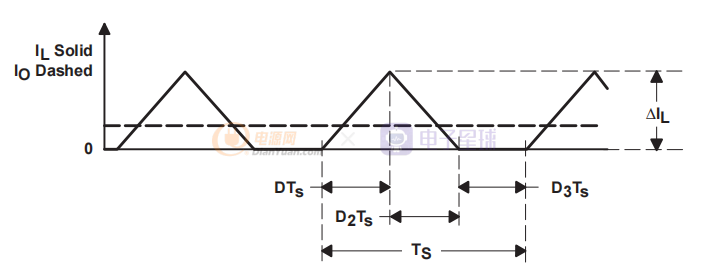
圖5 完全斷續DCM
要開始推導非連續傳導模式降壓功率級電壓轉換比,請觀察功率級在非連續電流模式操作期間呈現的三種獨特狀態。 ON 狀態是當 Q1 為 ON 且 CR1 為 OFF 時。 OFF 狀態是當 Q1 為 OFF 且 CR1 為 ON 時。 IDLE 狀態是當 Q1 和 CR1 都關閉時。 前兩種狀態與連續模式情況相同,圖 2 中的電路適用,但 TOFF ≠ (1–D) × TS。 開關周期的剩余部分是空閑狀態。 此外,輸出電感的直流電阻、輸出二極管正向壓降和功率 MOSFET 導通狀態壓降都假設小到可以忽略不計。
導通狀態的持續時間為 TON = D × TS 其中 D 是占空比,由控制電路設置,表示為開關導通時間與一個完整開關周期時間 Ts 的比率。 OFF 狀態的持續時間為 TOFF = D2 × TS。 空閑時間是開關周期的剩余時間,其公式為 TS – TON– TOFF = D3 × TS。 這些時間用圖 6 中的波形顯示。
不用像前面那樣詳細解釋,下面給出電感電流增加和減少的公式。
導通狀態期間電感電流的增加由下式給出:
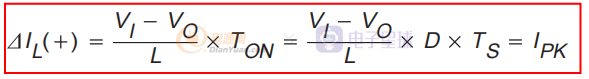
紋波電流幅值 ?IL(+) 也是峰值電感電流 Ipk,因為在不連續模式下,每個周期的電流從零開始。OFF 狀態期間電感電流的下降由下式給出:
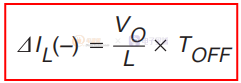
在連續導通模式的情況下,導通時間期間的電流增加 ?IL(+) 和關斷時間期間的電流減少 ?IL(–) 是相等的。因此,這兩個方程可以相等并求解 為 VO 獲得用于求解電壓轉換比的兩個方程中的第一個:

現在我們計算輸出電流(輸出電壓 VO 除以輸出負載 R)。 它是電感電流的平均值。

現在,將 IPK 的關系代入上式得到:
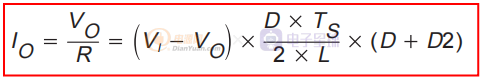
我們現在有兩個等式,一個是剛導出的輸出電流,另一個是輸出電壓(上圖),均以 VI、D 和 D2 表示。 我們現在求解 D2 的每個方程,并使這兩個方程彼此相等。 使用得到的方程,可以推導出輸出電壓 VO 的表達式。
非連續導通模式降壓電壓轉換關系由下式給出:
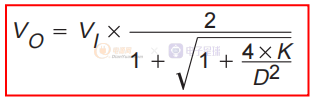
其中 K 定義為:

上述關系顯示了兩種傳導模式之間的主要區別之一。 對于非連續導通模式,電壓轉換關系是輸入電壓、占空比、功率級電感、開關頻率和輸出負載電阻的函數,而對于連續導通模式,電壓轉換關系僅取決于輸入電壓和 占空比。
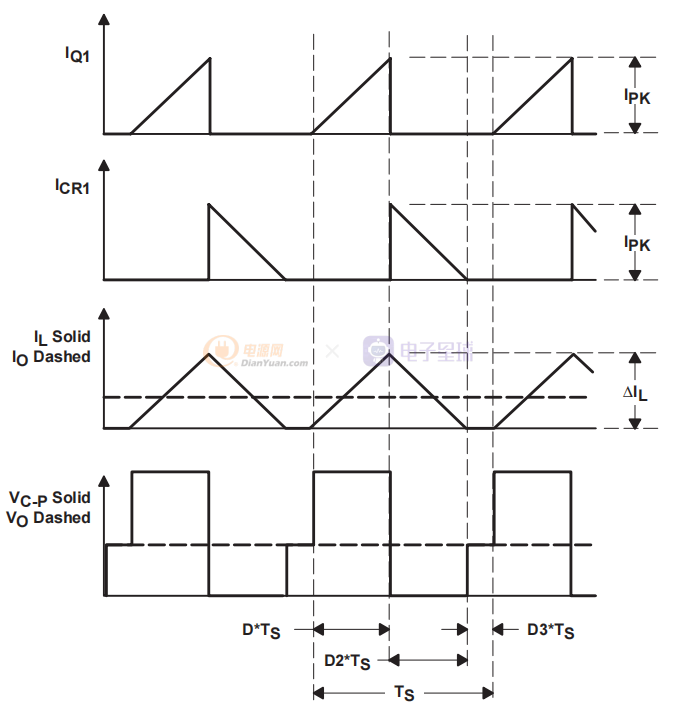
圖6 DCM工作波形
應該注意的是,降壓功率級在正常情況下很少在不連續導通模式下運行,但只要負載電流低于臨界水平,就會出現不連續導通模式。
下一節我們將討論如何計算相關參數。


