輸出電容不同于AC/DC應用中的母線電容，其與電路拓撲、工作狀態、ESR電阻及開關頻率等都有關，在這錯綜復雜的關系中也存在著共性，下面就準備逐一展開分析并試圖找出反激電路輸出電容的估算方法。

首先假設ESR電阻為零的情況

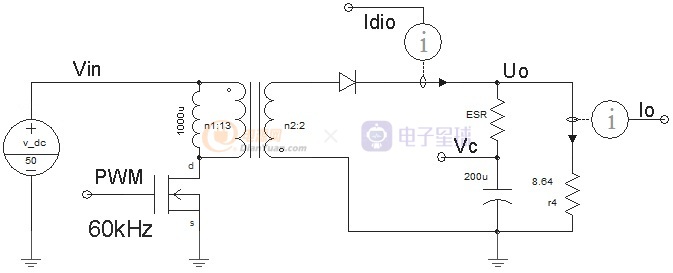
圖1-1 反激電路

  按圖1-1中的參數可以得到如下的波形曲線：

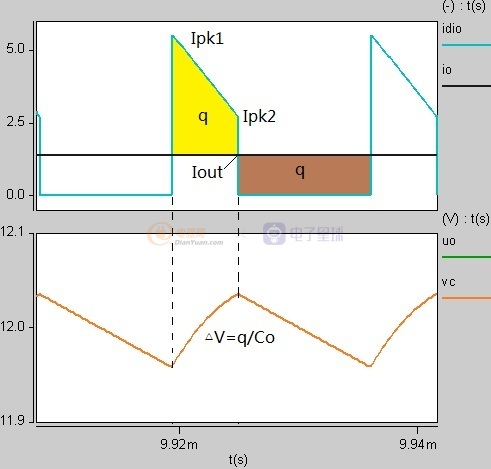
圖1-2 深連續模式下的電流及紋波波形

  圖1-2中的電壓紋波可以通過對輸出二極管的電流積分獲得，但工程應用中并不需要知道精確的波形軌跡只需求出峰值紋波即可，峰值紋波滿足公式△V=q/Co所以求出電荷量q就能估算出紋波大小而不用積分運算。

  圖1-2中黃色區域q為充電電荷棕色區域q為放電電荷，穩態時二者面積相同所以無論采用哪一邊的q進行計算都可以，這里顯然采用右邊棕色區域計算更為簡單電量q=Io*Don*T這樣就得到了輸出紋波電壓的第一種狀態表達式：

△V=q/Co=Io*Don/(Co*f)

  當把輸入電壓調至70V又會獲得如下波形曲線：

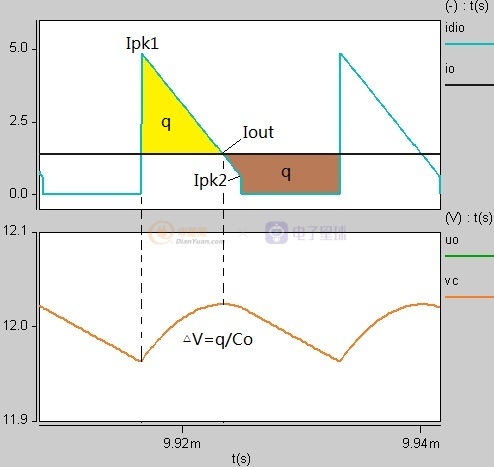
 圖1-3 淺連續模式的電流及紋波波形

  圖1-3依然滿足公式△V=q/Co，此時左側黃色區域似乎更容易求解。對黃色面積求解可以有多種表達形式這里引入電流紋波率r=△I/Iavg=2*(Ipk1-Ipk2)/(Ipk1+Ipk2)，這樣就得到了輸出紋波電壓的第二種狀態：

△V=q/Co=Io*（2*Don+r）^2/(Co*f*8*r) 

  第一種狀態和第二種狀態的分界線為

r=2*Don

  將輸入電壓繼續調大至大于100V電路進入斷續模式后紋波不在變化，此時依然可以按照公式△V=q/Co求解，表達式也可以有多種形式這里引入峰值電流Ipk得到輸出紋波電壓的第三種狀態：

△V=q/Co=Io*（Io+Ipk）^2/(Co*f*Ipk^2)

第二種和第三種狀態的分界線為

r=2

將反激的三種狀態公式匯總一下（ESR=0）

之后可以分析出一個等功率反激電路輸出紋波隨著輸入電壓從小到大變化的規律。

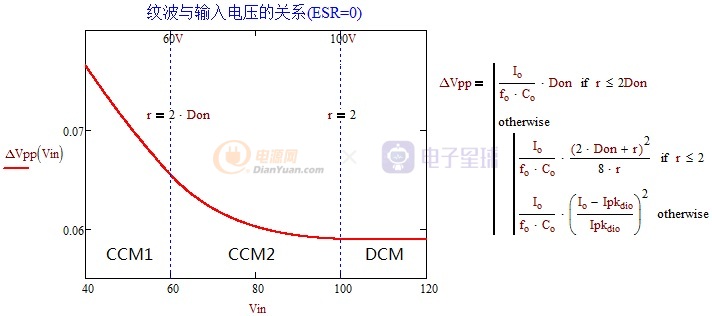
圖1-4 輸出紋波與輸入電壓的關系（ESR=0）

  圖中同時也給出了三種狀態的分界線，可知在ESR=0的條件下深連續模式下的輸出紋波最大，斷續模式時紋波最小且保持不變。

  其次考慮ESR電阻不為零的情況，由于ESR電阻上產生的壓降是下降趨勢而濾波電容上的電壓是上升趨勢所以最后的紋波不能用估算法直接疊加而是選擇其中最大的組合方式。

淺連續或者DCM模式時

如果(Ipk1-Io)*ESR>△Vpp 則輸出紋波為Ipk1*ESR，

如果(Ipk1-Io)*ESR<△Vpp 則輸出紋波為Io*ESR+△Vpp

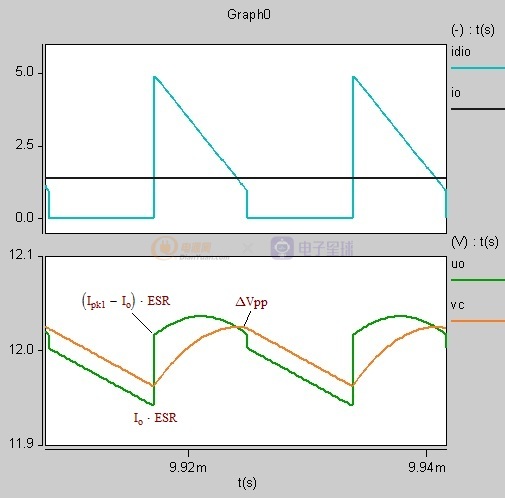
 圖1-5-1 淺連續模式

深連續模式時

如果Ipk1*ESR>△Vpp+Ipk2*ESR 則輸出紋波為Ipk1*ESR

如果Ipk1*ESR<△Vpp+Ipk2*ESR 則輸出紋波為Ipk2*ESR+△Vpp

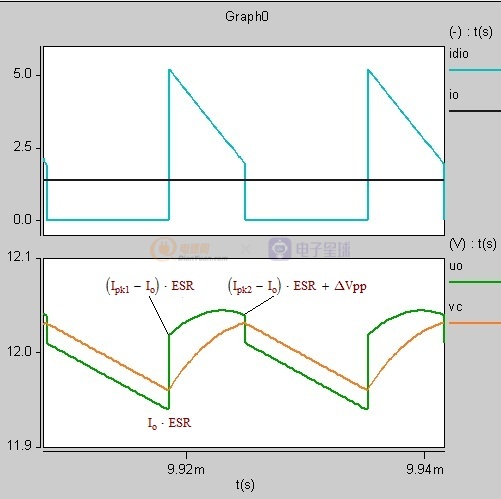
 圖1-5-2 深連續模式

  前面假設電容紋波曲線為直線（實為弧線）所以結果存在一定的誤差，當ESR電阻較大峰值電流Ipk*ESR遠大于電容紋波時這一誤差就消除了，見下圖

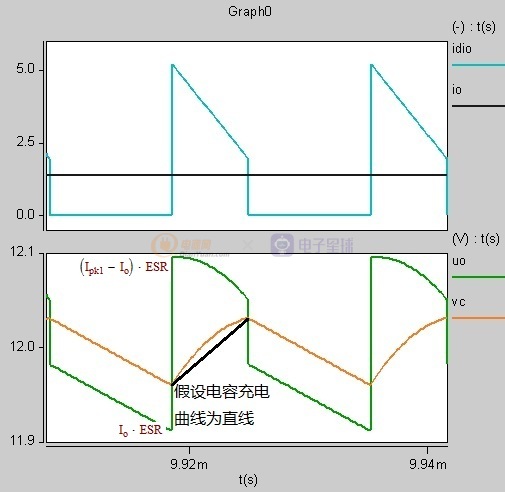
 圖1-5-3 ESR較大時的波形

 根據上述各種情況繪制出不同ESR的曲線圖如下

圖1-6 不同ESR下輸出紋波與輸入電壓的關系

  當ESR紋波=電容紋波時可以計算出臨界條件，以深連續模式為例（輸入電壓50V）根據公式

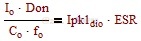
  計算出ESR=0.005，設Gesr=ESR*Co可知當前條件下臨界Gesr=0.1*10^-6。

  對于電解電容一般Gesr=60*10^-6，根據公式可以計算出當前條件下電解電容的臨界頻率為2.7kHz左右，通常開關電源頻率都在幾十kHz以上所有如果輸出采用的是電解電容可以直接用輸出峰值電流乘以ESR電阻來估算（Ipk1*ESR），至此實現了反激電路最小輸出電容的估算。