摘要:提出了一種新的基于滑模控制的正弦波逆變器。該逆變器采用了兩組對稱的Buck電路,并利用滑模控制對系統參變量變化和外部擾動的不敏感性及魯棒性。該逆變器能獲得一個較為理想的正弦輸出電壓。給出了電路的工作原理和滑模控制方案,并進行了仿真和實驗研究。
關鍵詞:逆變器;滑模控制;Buck變換器
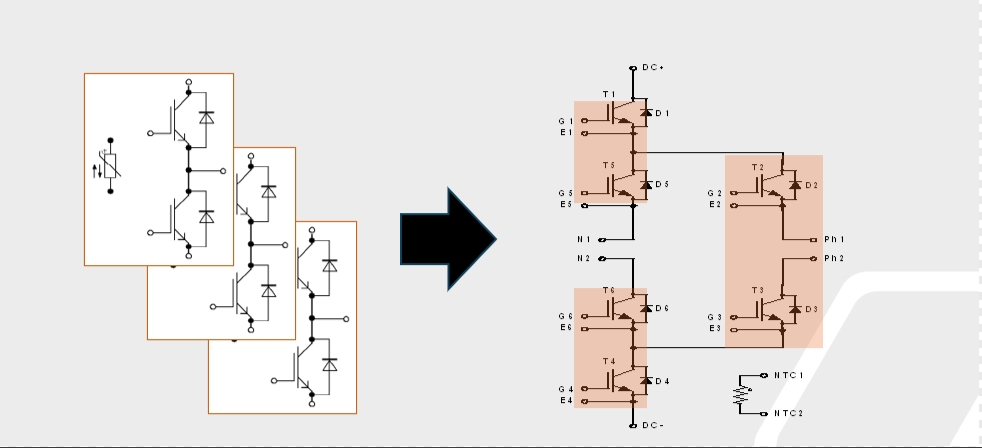
圖1正弦波逆變器電路基本拓撲
1引言
DC/AC變換技術發展迅速,并已經在越來越多的領域中得到應用。傳統的DC/AC變換器主電路的拓撲多采用推挽式、半橋式和全橋式等。控制方法上一般采用PWM控制并在輸出端加LC濾波,另一種常用的方法是采用SPWM控制。與之相比,建立在諧波消除技術上的最優PWM控制能獲得更好的正弦波輸出電壓。但是在負載變化的情況下,這些PWM方法無法保證輸出電壓的理想特性。瞬時反饋控制被提出來解決這個問題[1],但是這種控制方法對系統參變量的擾動比較敏感。在一些關鍵的應用場合中,往往要求DC/AC變換器的輸出電壓具有理想的正弦波特性。本文提出了一種新的正弦波逆變器電路拓撲,它由兩組對稱的Buck電路組成,并采用滑模控制方案,從而獲得平滑的正弦波輸出電壓。滑模控制相對于傳統的控制方案的主要優勢在于其所具有的參變量的魯棒性,它對系統參變量的擾動和負載的變化都具有不敏感性,具有良好的動態和穩態響應[2]。
2電路基本結構與工作原理
本文提出的正弦波逆變器電路基本拓撲如圖1所示。采用了兩組對稱的Buck電路,負載跨接在兩個Buck變換器的輸出端,并以正弦的方式調節Buck變換器的輸出電壓,從而進行DC/AC的變換。它包括直流供電電源Vin,輸出濾波電感L1和L2,功率開關管S1~S4,濾波電容C1和C2,續流二極管D1~D4,以及負載電阻R。通過滑模控制,使輸出電容電壓V1和V2隨參考電壓的變化而變化,從而使兩個Buck變換器各產生一個有相同直流偏置的正弦波輸出電壓,并
圖2雙向Buck變換器
圖3滑模控制器基本框圖
且V1和V2在相位上互差180°。由于負載跨接在V1和V2的兩端,則DC/AC變換器的輸出電壓V0如式(1)所示。(1)
雖然有一個直流偏置電壓出現在負載的任一端,但負載兩端電壓為正負交變的正弦波電壓,并且其直流電壓為零。由于DC/AC變換器的輸出電流是正負交變的,因此要求電路中的Buck變換器的電流能雙向流通,如圖1所示電路由兩組雙向Buck變換器組成。
一組電流雙向流通的Buck變換器可見圖2所示。S1與S2是一對互補控制的開關管,D1和D2為反并二極管。當開關S1閉合,S2打開時,若電感電流方向為正,則電流流經S1,若為負,則電感電流經D1續流。當S1打開,S2閉合時,若電感電流方向為正,則電流經D2續流,若為負,則電感電流流經S2。
3滑模控制器的設計
在本文中正弦波逆變器的控制采用了滑模控制器。由于電路中的兩個雙向Buck變換器是對稱的,并且具有獨立性,下面僅對一個雙向Buck變換器(圖2所示)的控制進行分析。控制框圖如圖3所示。vc與iL分別為輸出電容電壓反饋信號和輸出電感電流反饋信號。為了保證滑模控制的魯棒性,參考電流定義由式(2)所示[3]:iLref=i0+C(2)
為獲得輸出電壓的良好的瞬態響應,以狀態變量偏差(根據參考變量的差定義)的線性組合來表示的狀態空間的滑動平面方程由式(3)給出:
s(x)=c1x1+c2x2(3)
這里系數c1和c2是增益,x1是輸出電容電壓偏差,x2是輸出電感電流偏差,可表示為式(4)、式(5):
x1=vc-vref(4)x2=iL-iLref=iL-i0-C=ic-C(5)
式中C為輸出電容值。從式(5)可知,需同時檢測電感電流和負載電流,事實上兩者之差即為電容電流,所以只需檢測電容電流即可。式(5)可變為:x2=ic-C(6)其中ic為電容電流的反饋信號,相應的參考電流變為C。所以得:s(x)=c1(vc-vref)+c2(ic-C)(7)
信號s(x)通過一個滯環比較器產生開關管的控制信號。通過閉環控制,使得變量s(x)接近于零,系統達到穩定狀態。系統的響應由電路參數和控制參數c1與c2決定。合適地選擇這些參數,可以獲得較高的控制魯棒性、穩定性以及較快的響應速度。
圖2所示電路中,定義變量γ如下:γ=(8)
以電感電流iL與電容電壓vc為狀態變量,可得雙向Buck電路的狀態空間方程為:=+γ(9)
可簡寫為:=Ay+Bγ(10)
式中y=A=B=
控制技術
根據變結構系統理論,變換器方程可改寫為:=A′x+B′γ+D(11)
x=y-y*(12)式中x為狀態變量誤差,x=,y*=。代入式(12)得:
iL=x1+iLref(13)
vc=x2+vref(14)
將式(2)代入式(13)并考慮i0=vc/R,得:iL=x1++icref(15)式中icref=C(16)
將式(14),(15)與(16)代入式(9)得:=++γ(17)
對照式(11)可得:A′=B′=(18)D=
改寫式(3)為
s(x)=c1x1+c2x2=cTx(19)式中cT=,x=。
滑模存在的條件是要求所有在滑模面附近的狀態軌跡都指向滑模面。通過滑模控制器產生的信號控制開關管的動作來保證系統的狀態穩定在滑模面附近。因此滑模控制器需滿足式(20):(20)
使開關管變量γ有如式(21)所示關系時,滿足式(20)。γ=(21)
因此式(20)所表示的條件也可改寫為:(22)
在實際應用中,可以認為狀態變量誤差x遠遠小于參考量y*,因此式(22)可變為:(23)
將B′與D代入得:(24)
式(16)代入式(24)得:(25)
當系統穩定時,式(7)等于零,可得電壓誤差的動態特性為:=-(26)在一個穩定的滑模控制中,必須滿足>0。結合式(25),可得:
c1>0,c2>0(27)
設計一個有效的滑模控制器,就必須同時滿足式(25)與式(27)兩個條件。
理論上閉環滑模控制的變換器具有無限高的開關頻率,但在具體實現時是不可能的,因為過高的開關頻率會產生高頻顫動,這種高頻顫動會在系統中形成干擾,使系統不穩,同時高頻顫動也增加了開關損耗。為了回避這種高頻顫動,需要采取相應的開關頻率降低方法,本文采用了延遲方法,即式(21)修改為:γ=(28)
式中σ為控制延遲量,當-σ 本變換器的滑模控制器如圖4所示。該控制器的c1=0.3226,c2=0.2036;電流反饋系數k=0.08V/A;選取L=200μH,C=220μF。 圖5~圖7所示為負載R=100Ω時的電路仿真結果。Vin=200V,正弦參考電壓vref=2+sin314t。從 一種基于滑模控制的正弦波逆變器 圖8負載突變時輸出電流波形和輸出電壓波形(仿真) (b)輸出電壓 圖9輸出電壓波形(實驗) (a)輸出電流 圖中波形可知,電壓v1=62+31sin314t,電壓v2=62-31sin314t,變換器的輸出電壓v0=v1-v2=62sin314t。圖8為負載R從空載到R=10Ω時的輸出電壓。從圖中可知,當負載突變時輸出電壓變化很小。 圖9所示為負載R=100Ω,Vin=50V時的實驗結果。 5結論 本文提出了一種新的正弦波逆變器的電路拓撲,闡述了其工作原理,并基于滑模控制原理設計了電路的控制方案。從仿真和實驗結果可知此電路能較好地實現DC/AC變換,系統具有良好的動態和穩態響應。與傳統的全橋SPWM電路相比,能獲得更為理想的正弦輸出電壓。并且由于電感L和電容C是Buck電路的濾波元件,因此可以使用高頻電感以及大的電解電容作為濾波元件,從而可以減小電感值以及電感體積。此外,該電路也能較好地跟蹤非正弦給定信號,因而也可用于信號的功放。本方案的缺點是需采用兩組控制器,控制電路相對較為復雜。
聲明:本內容為作者獨立觀點,不代表電源網。本網站原創內容,如需轉載,請注明出處;本網站轉載的內容(文章、圖片、視頻)等資料版權歸原作者所有。如我們采用了您不宜公開的文章或圖片,未能及時和您確認,避免給雙方造成不必要的經濟損失,請電郵聯系我們,以便迅速采取適當處理措施;歡迎投稿,郵箱∶editor@netbroad.com。
| 微信關注 | ||
 |
| 技術專題 | 更多>> | |
 |
| 技術專題之EMC |
 |
| 技術專題之PCB |